В качестве примера фазового перехода первого рода рассмотрим переход жидкость - насыщенный пар. Для его описания применим термодинамический метод циклов. С. Карно показал, что КПД идеального обратимого цикла Карно не зависит от рода рабочего тела и определяется только температурами нагревателя и холодильника. Поэтому построим цикл Карно, взяв в качестве рабочего тела 1 моль реального газа.
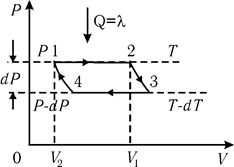 Рис. 10.11 Рис. 10.11 |
Схема цикла изображена на рис. 10.11. В начальной точке 1 вещество находится в жидком состоянии. При изотермическом расширении 1®2 жидкость превращается в насыщенный пар, поглощая некоторое количество теплоты от нагревателя. В точке 2 всё вещество превратилось в насыщенный пар (при температуре Т). В результате перехода 1®2 жидкость поглотила теплоту, равную молярной теплоте испарения Q=l. Теперь проведем бесконечно малое адиабатное расширение, вследствие чего температура рабочего тела упадет до T - dТ, а давление до Р - dР (точка 3). Далее проведём изотермическое сжатие пара до точки 4, после чего вернемся в исходную точку с помощью адиабатного сжатия 4®1. КПД цикла
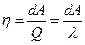 . . |
Поскольку работа равна площади, ограниченной циклом, то
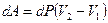 , , |
где V2 и V1 – молярные объёмы соответственно насыщенного пара и жидкости.
Таким образом,
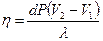 . . | (10.1) |
С другой стороны, КПД рассматриваемого цикла Карно
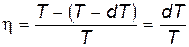 . . | (10.13) |
Приравняв (10.12) к (10.13), получим уравнение Клапейрона-Клаузиуса:
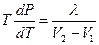 . . | (10.14) |
Можно показать, что это уравнение справедливо для любых фазовых переходов первого рода, только в каждом конкретном случае необходимо использовать соответствующие значения теплоты перехода и объёмов сосуществующих фаз.
Используем уравнение Клапейрона-Клаузиуса для установления зависимости давления насыщенного пара от температуры. Предварительно сделаем некоторые упрощающие допущения.
А. Будем считать, что молярная теплота испарения постоянна и не зависит от температуры.
Б. Объем насыщенного пара значительно больше объема жидкости, т.е. V2 – V1» V2, объем насыщенного пара примем 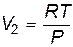 , считая его идеальным газом.
, считая его идеальным газом.
С учетом этих допущений уравнение (10.14) принимает вид
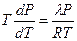 . . |
Разделив переменные и проинтегрировав, получим
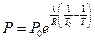 . . | (10.15) |
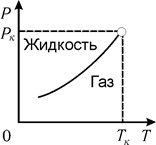 Рис. 10.12 Рис. 10.12 |
Полученное выражение достаточно хорошо описывает зависимость Р (Т) вдали от критической точки.
На рис. 10.12 показана зависимость Р (Т) при фазовом переходе жидкость - насыщенный пар, построенная с помощью (10.15.). Выше этой кривой размещена область жидкого состояния, а ниже – газообразного. В точках, лежащих на кривой, значения давления и температуры соответствуют равновесному сосуществованию насыщенного пара и жидкости. Кривая равновесия обрывается в критической точке.
Известно, что твердое тело может непосредственно превращаться в пар (этот процесс называется возгонкой, или сублимацией). Такой процесс также описывается уравнением Клапейрона-Клаузиуса. Возможно также равновесное сосуществование твердой и жидкой фаз.
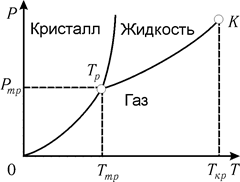 Рис. 10.13 Рис. 10.13 |
Обобщая изложенное, можно построить общую диаграмму состояний (рис. 10.13). На этой диаграмме кривые равнодействия выделяют области отдельных фазовых состояний.
Все три кривые равновесия пересекаются в одной точке, определяющей значения давления Р и температуры Т, при которых твердая, жидкая и газообразная фазы находятся в равновесии. Эта точка называется тройной.
 2015-02-04
2015-02-04 1313
1313