Определение. Две группы G и G' с операциями 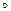и называются изоморфными, если существует отображение f : G G' такое

Две группы G и G' с операциями и 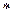называются изоморфными, если существует отображение f: G 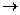G' такое, что:

а) f (a 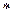b)=f(a) 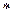f(b) для всех a,b 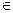G;

б) f – биективно. Обозначение изоморфных групп 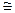G G'.

Простейшие свойства изоморфизма:

а) Единица переходит в единицу.

б) f(а^-1)=f^--1(a).

в) Обратное отображение f^—1 : G' 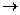G, существующее в силу свойства б), тоже является изоморфизмом.

В качестве изоморфного отображения f мультипликативной группы (R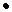₊, ) положительных вещественных чисел на аддитивную группу (R, +) всех вещественных чисел служит f:=ln.

Известное свойство ln ab=ln a + ln b моделирует свойство а) в определении изоморфизма. Обратным к f служит отображени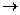е х е^х.

Рассмотрим две теоремы иллюстрирующие роль изоморфизма в теории групп.

Теореме 3.

Все циклические группы одного и того же порядка (в том числе и бесконечного изоморфны).