Гомоморфизм

В группе автоморфизмов Aut (G) группы G содержится одна особая подгруппа I_nn(G) иназывается группой внутренних автоморфизмов.Ее элементами являются отображения I_а:q 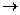aga^-1. Легко показать, что I_а действительно удовлетворяет всем свойствам требуемым от автоморфизмов, причем I_а=I 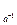, Ie=1- единичный автоморфизм, Ia 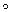Ib=Iab, так как (Ia 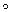Ib)(g) =I_a(I_b(q))=I_a(bgb^-1)=abgb^-1a^-1=abg(ab)^-1=I_ab(g).

Последнее соотношение показывает, что отображение

f: G 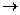I_nn(G)

G на группу I _nn(G) ее внутренних автоморфизмов определяется формулой f(a)=Ia,a 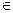G обладает свойством а) изоморфного отображения f(a) 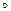f(b)=f(a,b). Свойство б) при этом необязано выполняеться. Если, например, G абелева группа, то aga^-1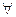= g а,g 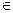G, так что I_a= I_е и вся группа I_nn(G) состоит из одного единичного элемента Ie.