Циклические группы

Пусть G мультипликативная группа (то есть с операцией умножения), а - ее фиксированный элемент. Если любой элемент g 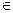G записывается в виде g = а ⁿ для некоторого n 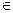Z, то говорят, что G = 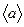- циклическая группа с образующим а (или циклическая группа, порожденная элементом а). Аналогично циклическая группа определяется в аддитивном случае: 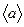={na|n 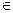Z}. Это конечно не означает, что все элементы аⁿ или аn попарно различны. Условимся обозначать (а^-1) ^k = a ^–k .