Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Тульский государственный университет»
Политехнический институт
Кафедра «Инструментальные и метрологические системы»
СБОРНИК МЕТОДИЧЕСКИХ УКАЗАНИЙ
К ЛАБОРАТОРНым РАБОТам
По дисциплине
Информатика
Направление подготовки:
221700 «Стандартизация и метрология»
Профиль подготовки: «Метрология и метрологическое обеспечение»
Форма обучения:очная
Тула 2012 г.
Методические указания к лабораторным работам составлены доцентом Е.В. Сорокиными обсуждены на заседании кафедры «Инструментальные и метрологические системы»факультета механико-технологического.
протокол №___ от "___"____________ 20___ г.
Зав. кафедрой ________________ О.И. Борискин
Методические указания к лабораторным работам пересмотрены и утверждены на заседании кафедры «Инструментальные и метрологические системы» факультета механико-технологического.
протокол №___ от "___"____________ 20___ г.
Зав. кафедрой ________________ О.И. Борискин
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего профессионального образования
«Тульский государственный университет»
Политехнический институт
Кафедра «Инструментальные и метрологические системы»
К ЛАБОРАТОРНОЙ РАБОТЕ №1
Системы счисления
По дисциплине
Информатика
Направление подготовки:
221700 «Стандартизация и метрология»
Профиль подготовки: «Метрология и метрологическое обеспечение»
Форма обучения:очная
Тула 2012 г.
Перевод чисел из одной системы счисления в другую
Системой счисления называется совокупность символов, используемых для изображения чисел, т.е. кодирования числовой информации.
Системы счисления делятся на позиционные и непозиционные.
В непозиционной системе счисления местоположение символа определяющего цифру (число) не оказывает влияние на размер числа.
Примером такой системы является Римская система счисления.
Символы используемые в Римской системе счисления отображения чисел:
I - 1, V - 5, X - 10, L - 50, C - 100
Правило записи чисел: значение числа определяется суммой всех значений символов, расположенных правее максимального числа за вычетом значений символов, расположенных левее данного символа.
Примеры:
III (3), IV (4), XXII (22), XLI (41), LXXXIII (83)
Количество цифр применяемых в позиционной системе счисления называется основанием системы счисления p. Местоположение символа в числе называется разрядом, каждый разряд имеет свой вес.
В любой системе счисления число можно представить
Аn An-1 … A2 A1 A0, A--1 A-2 … A—m= An *pn + An-1 *pn-1 +…+ A2 *p2 + A1 *p1 + A0 *p0 + A-1 *p-1 + A-2 *p-2 +…+ A-m *p-m
Например:
345,16(10) = 3 * 102 + 4 * 101 + 5 * 100 + 1 * 10-1 * 6 * 10-2,
где (10) - основание десятичной системы счисления.
В вычислительной технике при кодировании информации широко используются двоичная, восьмеричная и шестнадцатиричная системы счисления, которые представлены в таблице 1.
Таблица 1
| Система счисления | |||
| двоичная | восмиричная | десятичная | шестнадцатиричная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Чтобы перевести число из одной системы счисления в другую необходимо разделить его на основание той системы в которую оно переводится, полученный остаток будет младшим разрядом числа в новой системе счисления, частное от деления делится на основание, остаток - следующий разряд и так далее, деление продолжается до тех пор пока не получится частное меньше основания системы в которую мы переводим - это будет старший разряд число в новой системе счисления.
Например, перевести число 351 из десятичной системы счисления в шестнадцатиричную и двоичную:
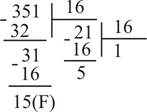
351(10) = 15F(16)
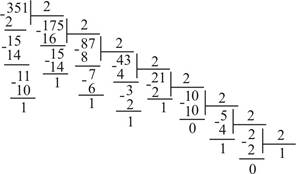
351(10) = 101011111(2)
Для перевода чисел из двоичной системы счисления в восьмеричную, шестнадцатиричную и наоборот можно воспользоваться следующим правилом: группа цифр из 3-х, 4-х двоичной системы заменяется на соответствующую цифру для восьмеричной, шестнадцатиричной системы и наоборот в соответствии с таблицей 2.
Например:
110 111 100 001(2) = 6741(8)
2305(8) = 010 011 000 101(2)
1111 0000 1011(2) = F0B(16)
577(16) = 0101 0111 0111(2)
Таблица 2
| Система счисления | |||
| двоичная | восьмиричная | двоичная | шестнадцатиричная |
| - | - | ||
| - | - | ||
| - | - | А | |
| - | - | В | |
| - | - | С | |
| - | - | D | |
| - | - | E | |
| - | - | F |
 2015-02-14
2015-02-14 1295
1295