Занятие 2. Уравнение Шредингера

Краткие теоретические сведения

Основные понятия

Одномерное временное уравнение Шредингера

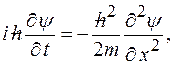
где 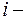мнимая единица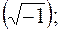 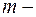масса частицы; 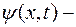волновая функция, описывающая состояние частицы.

Волновая функция, описывающая одномерное движение свободной частицы:

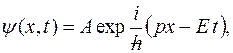
где 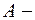амплитуда волны де Бройля; 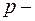импульс частицы; 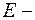энергия частицы.

Одномерное уравнение Шредингера для стационарных состояний:

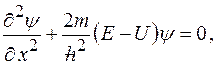
где 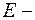полная энергия частицы; 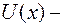потенциальная энергия; 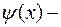координатная (или амплитудная) часть волновой функции.

Для случая трех измерений 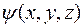уравнение Шредингера записывается в виде:

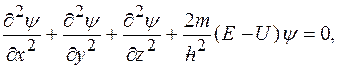
или в операторной форме:

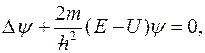
где 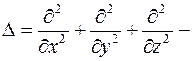оператор Лапласа.

Стандартные условия, которым должна удовлетворять волновая функция:

1) конечность (во всем пространстве; 2) однозначность; 3) непрерывность самой 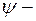функции и ее первой производной.

Вероятность 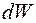обнаружить частицу в интервале от 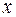до 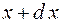(в одномерном случае) выражается формулой:

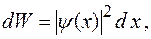
где 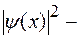плотность вероятности.

Вероятность 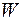обнаружить частицу в интервале от 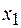до 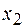находится интегрированием 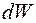в указанных пределах:

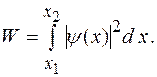
Собственное значение энергии 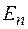частицы, находящейся на 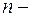м энергетическом уровне в бесконечно глубоком одномерном прямоугольном потенциальном ящике, определяется формулой:

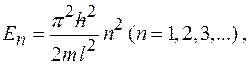
где 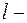ширина потенциального ящика.

Соответствующая этой энергии собственная волновая функция имеет вид:

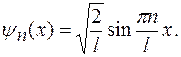
Коэффициент преломления 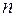волн де Бройля на границе низкого потенциального барьера бесконечной ширины (см Рис.1):

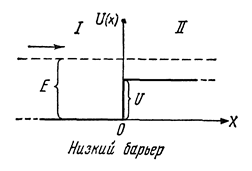
где 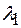и 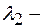длины волн де Бройля в областях I и II (частица движется из области I во II); 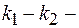соответствующие значения волновых чисел.

Коэффициенты отражения 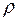и пропускания 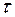волн де Бройля через низкий 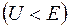потенциальный барьер бесконечной ширины:

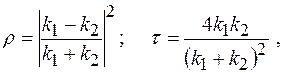
где 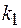и 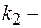волновые числа волн де Бройля в областях I и II.

Коэффициент прозрачности 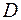прямоугольного потенциального барьера конечной ширины:

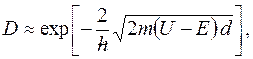
где 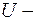высота потенциального барьера; 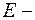энергия частицы; 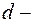ширина барьера.

Вопросы для ответа у доски

1. Каким свойствам должна удовлетворять волновая функция?

2. В чем заключается физический смысл волновой функции?

3. Для каких частиц справедливо уравнение Шредингера?

4. Почему уравнение Шредингера сформулировано как волновое уравнение?

5. Запишите временное и стационарное уравнение Шредингера и проанализируйте их.

6. Запишите одномерное временное и стационарное уравнения Шредингера и проанализируйте их.

Примеры решения задач:

Задача 1. Электрон находится в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной 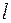. Вычислить вероятность того, что электрон, находящийся в возбужденном состоянии (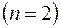, будет обнаружен в средней трети ящика.