Под заменой платежей понимают такое изменение условий ФО, при котором один платеж, имеющий будущую стоимость 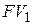 и срок погашения
и срок погашения 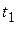 , заменяют новым платежом, имеющим будущую стоимость
, заменяют новым платежом, имеющим будущую стоимость 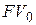 и срок погашения
и срок погашения 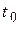 . Если при этом изменяют срок погашения
. Если при этом изменяют срок погашения 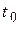 нового платежа по сравнению с ранее назначенным сроком
нового платежа по сравнению с ранее назначенным сроком 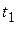 , то задача сводится к определению будущей стоимости
, то задача сводится к определению будущей стоимости 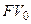 заменяющего платежа. В зависимости от используемой ставки можно выразить величину
заменяющего платежа. В зависимости от используемой ставки можно выразить величину 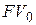 из соответствующего уравнения эквивалентности (6.2)–(6.5):
из соответствующего уравнения эквивалентности (6.2)–(6.5):
– при использовании простой процентной ставки
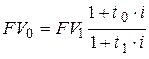 ; ; | (6.11) |
– при использовании сложной процентной ставки [2]
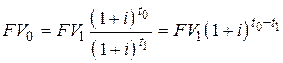 ; ; | (6.12) |
– при использовании простой учетной ставки
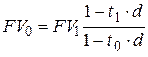 ; ; | (6.13) |
– при использовании сложной учетной ставки [2]
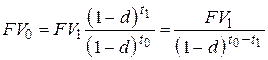 . . | (6.14) |
Полученные формулы показывают, что при увеличении срока 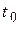 по сравнению с
по сравнению с 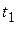 будет увеличиваться и будущая стоимость
будет увеличиваться и будущая стоимость 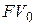 по сравнению с
по сравнению с 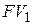 , а при уменьшении
, а при уменьшении 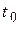 по сравнению с
по сравнению с 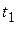 будущая стоимость
будущая стоимость 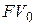 будет уменьшаться по сравнению с
будет уменьшаться по сравнению с 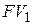 . Если сроки
. Если сроки 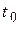 и
и 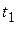 равны, то никакой замены не происходит и стоимости
равны, то никакой замены не происходит и стоимости 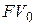 и
и 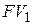 становятся равными.
становятся равными.
Если сроки погашения платежей 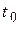 и
и 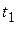 заданы в днях
заданы в днях 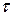 , то с учетом формулы (1.6) можно преобразовать, например, формулу (6.11):
, то с учетом формулы (1.6) можно преобразовать, например, формулу (6.11):
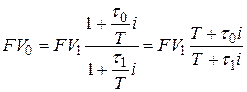 . . | (6.15) |
Каждая из формул (6.11)–(6.14), полученных на основе уравнений эквивалентности (6.2)–(6.5), содержит одновременно две операции: дисконтирование будущей стоимости 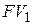 заменяемого платежа за период времени
заменяемого платежа за период времени 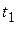 до его современной стоимости и наращение этой стоимости за новый период времени
до его современной стоимости и наращение этой стоимости за новый период времени 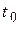 до величины новой будущей стоимости
до величины новой будущей стоимости 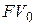 заменяющего платежа. При этом фактически происходит изменение стоимости
заменяющего платежа. При этом фактически происходит изменение стоимости 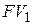 до
до 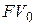 за дополнительный период времени
за дополнительный период времени 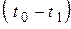 . Формулы (6.12) и (6.14) характеризуют это изменение нагляднее, чем формулы (6.11) и (6.13). Для повышения наглядности формул (6.11) и (6.13) обозначим
. Формулы (6.12) и (6.14) характеризуют это изменение нагляднее, чем формулы (6.11) и (6.13). Для повышения наглядности формул (6.11) и (6.13) обозначим 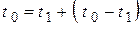 и, опустив элементарные преобразования этих формул, получим [5]:
и, опустив элементарные преобразования этих формул, получим [5]:
– при использовании простой процентной ставки
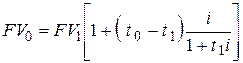 ; ; | (6.16) |
– при использовании простой учетной ставки
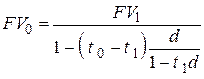 . . | (6.17) |
Структура формулы (6.16) соответствует структуре формулы (2.2) и показывает, что сумма 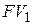 наращивается до суммы
наращивается до суммы 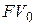 при величине скорректированной процентной ставки
при величине скорректированной процентной ставки 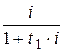 за период времени
за период времени 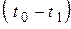 . Структура формулы (6.17) соответствует структуре формулы (2.16) и показывает, что сумма
. Структура формулы (6.17) соответствует структуре формулы (2.16) и показывает, что сумма 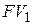 дисконтируется до суммы
дисконтируется до суммы 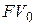 при величине скорректированной учетной ставки
при величине скорректированной учетной ставки 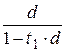 за период времени
за период времени 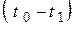 .
.
При изменении условий ФО участники могут прийти к соглашению об изменении будущей стоимости 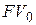 заменяющего платежа по сравнению с
заменяющего платежа по сравнению с 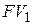 . Тогда задача сводится к определению срока погашения
. Тогда задача сводится к определению срока погашения 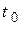 заменяющего платежа. Однако в соответствии с уравнением эквивалентности (6.1) сумма
заменяющего платежа. Однако в соответствии с уравнением эквивалентности (6.1) сумма 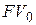 не может назначаться меньше приведенной стоимости
не может назначаться меньше приведенной стоимости 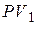 , которую можно определить из уравнений (6.2)–(6.5). Если это условие не будет выполнено, то получится отрицательное значение срока погашения
, которую можно определить из уравнений (6.2)–(6.5). Если это условие не будет выполнено, то получится отрицательное значение срока погашения 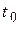 . В зависимости от используемой ставки можно выразить величину
. В зависимости от используемой ставки можно выразить величину 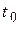 из соответствующего уравнения эквивалентности (6.2)–(6.5), причём для сложных ставок обе части уравнения после преобразований логарифмируют с использованием натуральных или десятичных логарифмов:
из соответствующего уравнения эквивалентности (6.2)–(6.5), причём для сложных ставок обе части уравнения после преобразований логарифмируют с использованием натуральных или десятичных логарифмов:
– при использовании простой процентной ставки
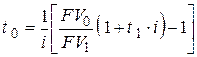 , , | (6.18) |
где 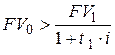 ;
;
– при использовании сложной процентной ставки [2]
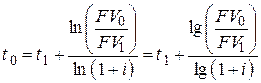 , , | (6.19) |
где 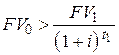 ;
;
– при использовании простой учетной ставки
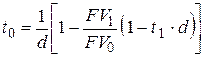 , , | (6.20) |
где 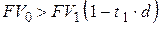 ;
;
– при использовании сложной учетной ставки [2]
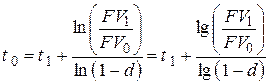 , , | (6.21) |
где 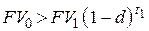 .
.
Если сроки погашения платежей 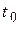 и
и 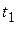 заданы в днях
заданы в днях 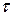 , то с учетом формулы (1.6) можно преобразовать, например, формулу (6.18):
, то с учетом формулы (1.6) можно преобразовать, например, формулу (6.18):
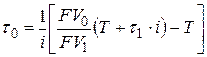 . . | (6.22) |
Формулы (6.19) и (6.21), нагляднее, чем формулы (6.18) и (6.20) показывают, что при изменении будущей стоимости 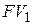 до величины
до величины 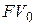 происходит изменение срока погашения от
происходит изменение срока погашения от 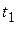 до
до 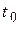 . Для повышения наглядности формул (6.18) и (6.20), выразим срок погашения
. Для повышения наглядности формул (6.18) и (6.20), выразим срок погашения 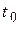 из формул (6.16) и (6.17) и получим [5]:
из формул (6.16) и (6.17) и получим [5]:
– при использовании простой процентной ставки
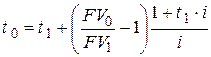 ; ; | (6.23) |
– при использовании простой учетной ставки
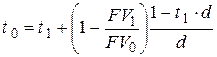 . . | (6.24) |
Пример 6.1. Платеж на сумму 25 000 рублей со сроком уплаты 8 мес. заменили новым платежом со сроком уплаты: а) 6 месяцев, б) 10 месяцев. Ставка наращения – 20% годовых. Определить сумму заменяющего платежа для четырех основных ставок (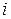 ,
, 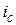 ,
, 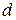 ,
, 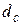 ).
).
 2015-02-14
2015-02-14 2546
2546








