Функция 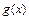 называется ограниченной по сравнению с функцией
называется ограниченной по сравнению с функцией 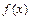 при
при  , если существует такая
, если существует такая
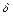 -окрестность точки
-окрестность точки 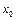 и такая постоянная
и такая постоянная 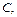 что как только
что как только 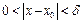 , тотчас выполняется
, тотчас выполняется 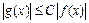 .
.
Для введенного понятия используется следующее обозначение: 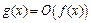 при
при  (читается так: «
(читается так: «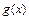 есть
есть 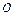 большое от
большое от 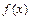 при
при  »).
»).
Знак  имеет здесь иной смысл, чем обычно, он лишь указывает на то, что рассматриваемое свойство имеет место только в некоторой окрестности точки
имеет здесь иной смысл, чем обычно, он лишь указывает на то, что рассматриваемое свойство имеет место только в некоторой окрестности точки 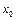 , но ни о каком пределе речь не идет.
, но ни о каком пределе речь не идет.
Аналогично определяется смысл записи 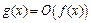 при
при 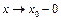 ,
, 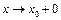 , x→∞, x→+∞, x→–∞.
, x→∞, x→+∞, x→–∞.
Если 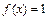 , то запись
, то запись 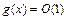 ,
,  означает, что в некоторой проколотой окрестности точки
означает, что в некоторой проколотой окрестности точки 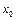 функция
функция 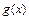 ограничена.
ограничена.
Пример 1. Верно ли: 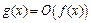 ,
,  , если
, если
1) 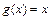 ,
, 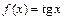 ,
,  ;
;
2) 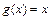 ,
, 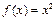 ,
, 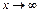 .
.
1) Используя известное неравенство 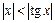 при
при 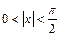 , получаем, что постоянное
, получаем, что постоянное 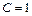 ,
, 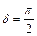 . Верно.
. Верно.
2) Для 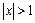 имеем:
имеем: 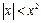 , следовательно, функция
, следовательно, функция 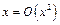 при
при 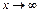 , хотя функция
, хотя функция 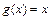 не является ограниченной при
не является ограниченной при 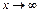 , она ограничена по сравнению с функцией
, она ограничена по сравнению с функцией 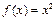
 .
.
 2015-02-14
2015-02-14 893
893








