Пусть 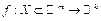 ,
, 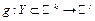 ,
, 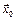 - предельная точка множества
- предельная точка множества 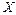 ,
, 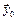 - предельная точка множества
- предельная точка множества 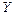 ,
, 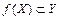 ,
, 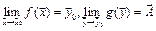 , при этом
, при этом 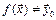 , если
, если 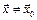 .
.
Тогда при 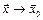 существует предел композиции
существует предел композиции 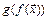 :
:
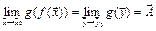 .
.
Эта теорема позволяет вычислять пределы, переходя от переменной 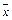 к новой переменной
к новой переменной 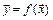 .
.
В случае непрерывности функции 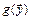 в точке
в точке 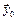 утверждение теоремы можно записать в виде формулы:
утверждение теоремы можно записать в виде формулы:
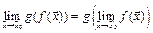 .
.
Пример 14. Найти 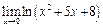 .
.
Применяя теорему о пределе композиции, будем иметь:
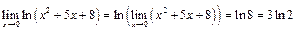 .
.
Понятие бесконечно малой (б.м.) и бесконечно большой (б.б.), их связь и леммы о бесконечно малых также могут быть использованы при отыскании пределов.
Определение бесконечно малой:
Функция 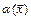 называется бесконечно малой функцией (или просто б.м.) при
называется бесконечно малой функцией (или просто б.м.) при 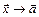 , если
, если 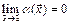 .
.
Справедливы леммы о б.м.
Лемма 1:
Если 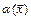 и
и 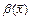 - б.м. при
- б.м. при 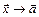 , а С1,С2 – вещественные числа, то
, а С1,С2 – вещественные числа, то 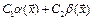 также б.м. при
также б.м. при 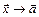 .
.
Лемма 2:
Если функция 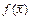 ограничена в окрестности точки
ограничена в окрестности точки 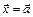 , а
, а 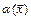 - б.м. при
- б.м. при 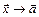 , то их произведение
, то их произведение 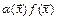 является б.м. при
является б.м. при 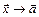 .
.
Определение бесконечно большой:
Функция 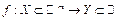 называется бесконечно большой при
называется бесконечно большой при 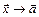 , если для
, если для 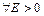
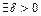 такое, что для
такое, что для 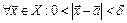 тотчас выполняется:
тотчас выполняется: 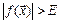 , т.е.
, т.е. 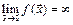 .
.
Связь между б.м. и б.б.:
Функция 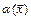 , отличная от нуля при
, отличная от нуля при 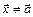 , является б.м. при
, является б.м. при 
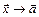 тогда и только тогда, когда обратная величина
тогда и только тогда, когда обратная величина 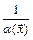 является б.б. при
является б.б. при 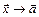 .
.
 Пример 15. Найти
Пример 15. Найти 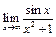 .
.
Функция 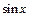 является ограниченной при
является ограниченной при 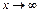 , ибо для
, ибо для 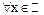 ,
, 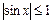 а функция
а функция 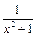 является б.м. при
является б.м. при 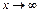 как величина, обратная б.б. функции (x2+1), следовательно, по лемме 2 о б.м.
как величина, обратная б.б. функции (x2+1), следовательно, по лемме 2 о б.м. 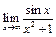 =0.
=0.
 Пример 16. Найти
Пример 16. Найти 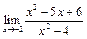 .
.
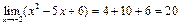 , а
, а 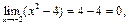 тогда
тогда 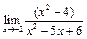 =0, откуда
=0, откуда 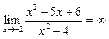 .
.
Возможны случаи, когда ни понятия непрерывности, ни теорема об арифметических свойствах предела, ни леммы о б.м. неприменимы, и необходимо рассматривать пределы неопределенных выражений. Так, если при 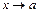 функции
функции 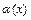 и
и 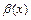 есть б.м.,
есть б.м., 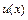 и
и 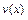 - б.б., а
- б.б., а 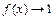 то возникают неопределенности, условно обозначаемые (1)
то возникают неопределенности, условно обозначаемые (1) 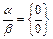 , (2)
, (2) 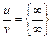 , (3)
, (3) 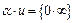 , (4)
, (4) 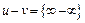 , (5)
, (5) 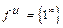 . Для раскрытия неопределенностей используются 1-й и 2-ой замечательные пределы и следствия из них:
. Для раскрытия неопределенностей используются 1-й и 2-ой замечательные пределы и следствия из них:
I. 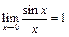 - 1ый замечательный предел;
- 1ый замечательный предел;
II. 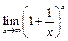 =
= 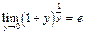 – 2ой замечательный предел;
– 2ой замечательный предел;
IIа. 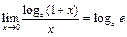 , IIб.
, IIб. 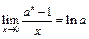 ,
,
IIв. 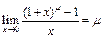 .
.
В примерах 17-43 найти пределы, раскрыв неопределённости.
Пример 17. 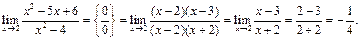
Пример 18. 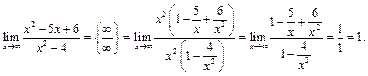
Пример 19. 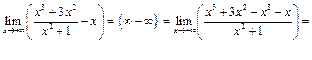
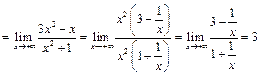 .
.
Пример 20. 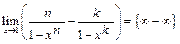 ,
, 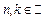 .
.
Сделаем замену переменной 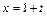 , тогда при
, тогда при 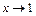 должно быть
должно быть 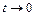 . Имеем:
. Имеем:
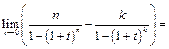
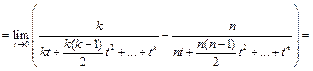
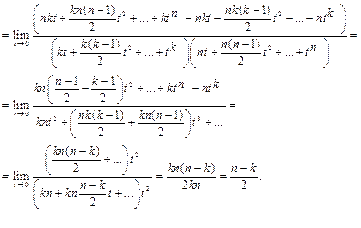

Пример 21. 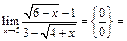
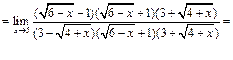
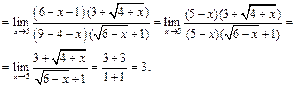
Пример 22.
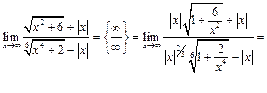
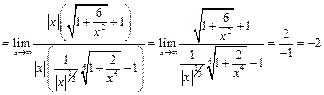 .
.
Пример 23. 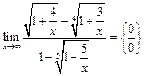 .
.
Делаем замену 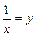 , если
, если 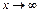 , то
, то 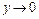 . Используем следствие IIв из 2го замечательного предела:
. Используем следствие IIв из 2го замечательного предела: 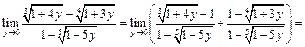
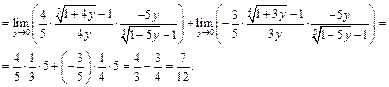
Пример 24. 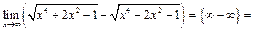
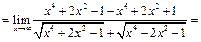
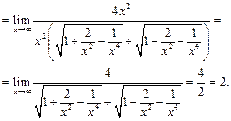
Пример 25. 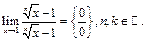
Делаем замену 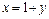 , если
, если 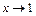 , то
, то 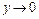 .
.
Тогда 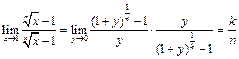 - c использованием следствия II в.
- c использованием следствия II в.
Пример 26. 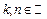
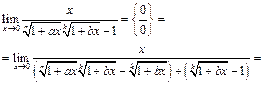
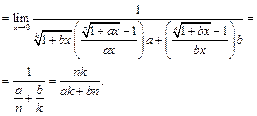
Пример 27. 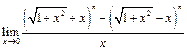
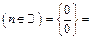
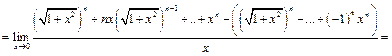
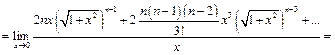
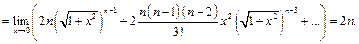
Пример 28. 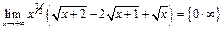 =
=
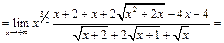
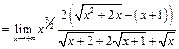
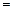
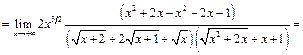
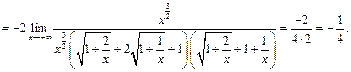
Пример 29. 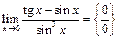 =
=
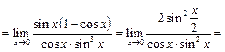
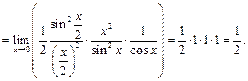
Пример 30. 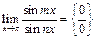 ,
, 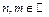 .
.
Делаем замену 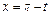 , если
, если  , то
, то 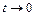 . Тогда
. Тогда 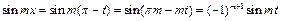 , поэтому
, поэтому 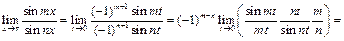
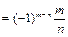 .
.
Пример31.
. 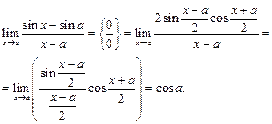
Пример 32. 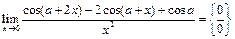 .
.
Так как 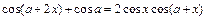 , то
, то 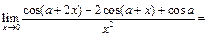
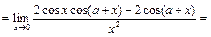
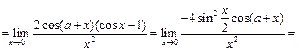
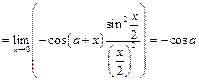 .
.
Пример 33.
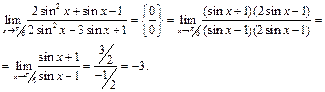
Пример 34. 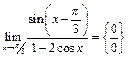 .
.
Учитывая, что:
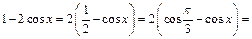
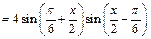 и
и
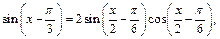 получим:
получим:
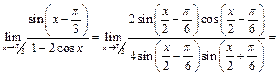
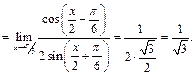
Пример 35.
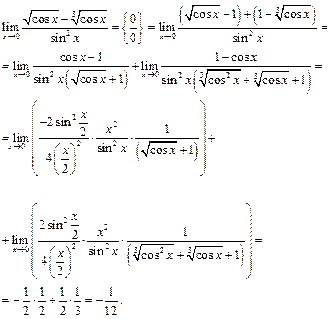
Пример 36. 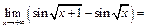
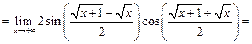
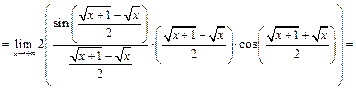
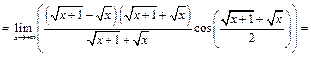
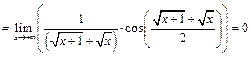 -
-
как произведение б.м. функции 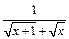 при
при 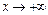 на ограниченную функцию
на ограниченную функцию 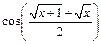 .
.
Пример 37.
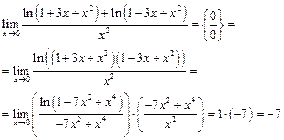
- с использованием следствия IIа.
Пример 38.
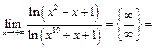
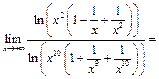
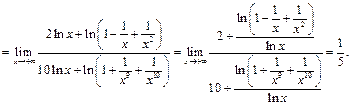
Пример 39. 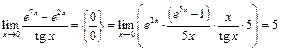 ,
,
используя следствие IIб.
Пример 40. 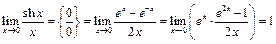 .
.
Пример 41.
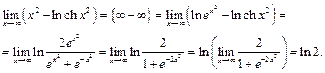
Пример 42. Для 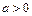
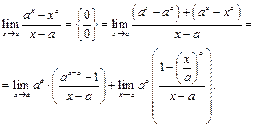
При вычислении первого из пределов используем следствие IIб, а во втором сделаем замену 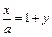 , если
, если 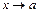 , то
, то 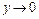 . Тогда
. Тогда
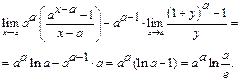
Пример 43.
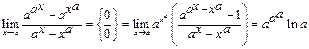 -
-
с использованием непрерывности степенной и показательной функций и следствия IIб.
Рассмотрим функцию вида: 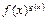 , называемую показательно-степенной. Данная функция непрерывна в любой точке
, называемую показательно-степенной. Данная функция непрерывна в любой точке 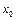 , где непрерывны функции
, где непрерывны функции 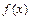 и
и 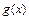 и где
и где 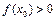 . Используя логарифмическое тождество
. Используя логарифмическое тождество 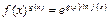 и теоремы о непрерывности композиции и произведения непрерывных функций, будем иметь:
и теоремы о непрерывности композиции и произведения непрерывных функций, будем иметь: 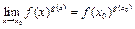 .
.
Но не всегда 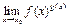 может быть найден непосредственно, он может представлять собой неопределённость, если
может быть найден непосредственно, он может представлять собой неопределённость, если 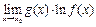 представляет неопределённость вида
представляет неопределённость вида 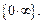 Это возможно в трёх случаях: 1)
Это возможно в трёх случаях: 1) 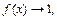
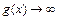 , 2)
, 2) 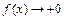 ,
, 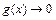 , 3)
, 3) 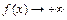 ,
, 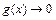 при
при  , и мы приходим к следующим типам неопределённостей:
, и мы приходим к следующим типам неопределённостей: 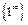 ,
, 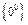 ,
, 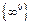 . Посредством использования логарифмического тождества эти неопределённости сводятся к более простой -
. Посредством использования логарифмического тождества эти неопределённости сводятся к более простой - 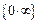 .
.
Пример 44. Найти 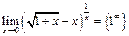 .
.
Неопределённость вида 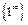 можно раскрывать с помощью 2–го замечательного предела. Покажем это:
можно раскрывать с помощью 2–го замечательного предела. Покажем это:
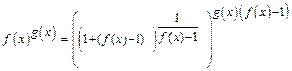
Положим далее 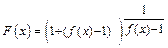 ,
,
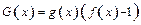 , тогда
, тогда 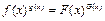 . Так как
. Так как 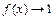 при
при 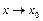 , то
, то 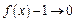 ,
, 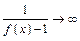 и тогда
и тогда 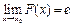 – по теореме о пределе композиции и с использованием 2-го замечательного предела. В силу непрерывности показательно- степенной функции получаем:
– по теореме о пределе композиции и с использованием 2-го замечательного предела. В силу непрерывности показательно- степенной функции получаем: 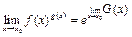 , при этом
, при этом 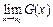 представляет неопределённость вида
представляет неопределённость вида 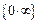 .
.
Итак, 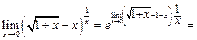
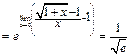 - с использованием следствия IIв
- с использованием следствия IIв
Пример 45. Найти 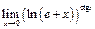 .
.
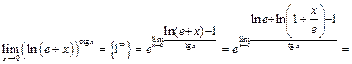

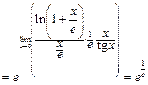 .
.
Пример 46. Найти 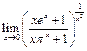 .
.
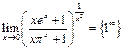
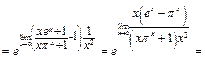
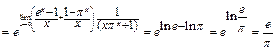 .
.
 2015-02-14
2015-02-14 7063
7063
