Определение непрерывности в предельной точке

Функция 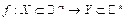называется непрерывной в предельной точке 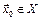, если .

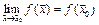Следовательно, для отыскания предела непрерывной в точке 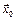функции достаточно найти значение функции в точке : .

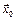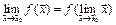Пример 12. Найти .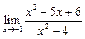

Используя понятие непрерывности и теорему об арифметических свойствах предела, получаем:

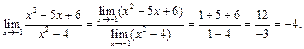
Пример 13.Найти .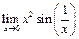

Пользуясь неравенством: 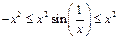и принципом двустороннего ограничения, получаем, что: .

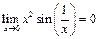При вычислении пределов применяется также