2015-02-14
664
Для того чтобы функци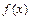и 
и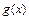 
были функциями одного порядка при 
, достаточно, чтобы при существовал конечный и не равный нулю предел отношения этих функций: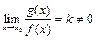 
.
Пример 2. Какие из следующих пар функций являются функциями одного порядка при 
:
1) 
, 
;
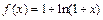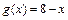2) 
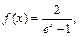
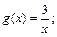
3) 
, 
;
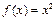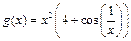4) , 
.
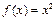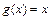1) Так как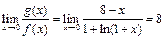 
, то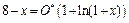 
, .
2) Учитывая, что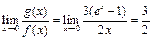 
, имеем: 
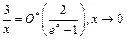. Отметим, что при обе функции являются бесконечно большими.
3) 
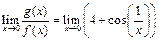не существует. Однако же данные функции являются при функциями одного порядка. Действительно, так как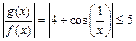 
при 
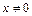, то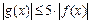 
, то есть 
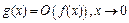. С другой стороны, 
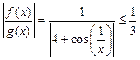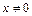, , то есть 
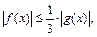и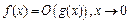 
. Итак, 
, 
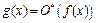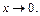
4) Воспользоваться теоремой нельзя, так как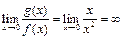 
.
Данные функции не являются функциями одного порядка при , так как, какова бы ни была постоянная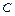 
, неравенство 
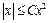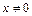, не выполняется ни в какой окрестности точки 
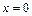, и функция 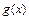не является ограниченной по сравнению с функцие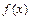й при .
Отметим, что пример 2.3 показывает: существование конечного предела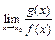 
достаточное, но не является необходимым условием того, что функци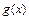и и 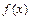одного порядка при .
