Определение 1. Функция 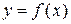 называется непрерывной в точке
называется непрерывной в точке  , если выполняются условия:
, если выполняются условия:
1)  определена в точке
определена в точке  и некоторой ее окрестности;
и некоторой ее окрестности;
2) существует 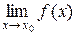 ;
;
3) этот предел равен значению функции в точке  :
: 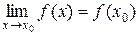 .
.
Определение 2. Функция 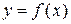 называется непрерывной в точке
называется непрерывной в точке  , если эта функция определена в некоторой окрестности точки
, если эта функция определена в некоторой окрестности точки  и если
и если
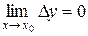 ,
,
т.е. бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Определение 3. Функция  называется непрерывной на отрезке (интервале), если она непрерывна в каждой точке данного отрезка (интервала).
называется непрерывной на отрезке (интервале), если она непрерывна в каждой точке данного отрезка (интервала).
Замечание (к определению 3). Существует понятие непрерывность слева (справа). В этом случае в исследуемых точках вычисляются односторонние пределы. Если не выполняется хотя бы одно из условий определений 1, 2, то функция  не будет непрерывна в точке
не будет непрерывна в точке  , и точка
, и точка  в этом случае называется точкой разрыва функции
в этом случае называется точкой разрыва функции  .
.
Точки разрыва принято подразделять на два типа.
Определение 4. Точка  (точка разрыва) называется точкой разрыва I-го рода функции
(точка разрыва) называется точкой разрыва I-го рода функции  , если существуют односторонние пределы этой функции при
, если существуют односторонние пределы этой функции при  слева и справа. Все остальные точки разрыва относятся к точкам разрыва II-го рода.
слева и справа. Все остальные точки разрыва относятся к точкам разрыва II-го рода.
Определение 5. Точка разрыва I-го рода  функции
функции  называется устранимой точкой разрыва, если существуют односторонние пределы функции
называется устранимой точкой разрыва, если существуют односторонние пределы функции  в точке
в точке  и они равны:
и они равны:
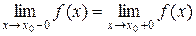 .
.
Если 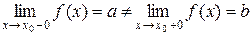 , то говорят, что функция
, то говорят, что функция  совершает в точке
совершает в точке  скачок на величину
скачок на величину 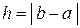 .
.
 2015-02-14
2015-02-14 577
577








