2015-02-14
2280
Теорема 1. Пусть функции 
и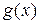 
определены в точке 
и некоторой ее окрестности. Тогда, если функции и 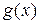непрерывны в точке , то функции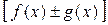 
, 
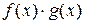будут также непрерывны в точке . Кроме того, если 
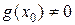, то функция 
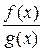непрерывна в точке .
Доказательство. Пусть функции и 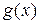определены в 
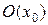и непрерывны в точке . Тогда 
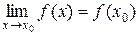и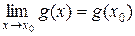 
. Из соответствующих свойств предела функции в точке получаем:
;
;
.
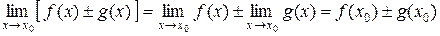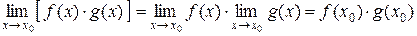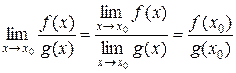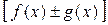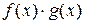Отсюда следует, что функции , и 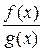непрерывны в точке .
Теорема 2. Пусть функция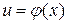 
непрерывна в точке и функция 
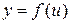непрерывна в точке 
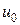, где 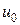– значение функции 
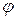в точке (
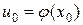), тогда сложная функция 
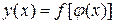будет непрерывна в точке .
Доказательство. Нужно доказать: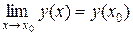 
.
По условию, функция 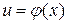непрерывна в точке . Это значит: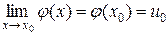 
. То, что 
, одновременно означает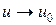 
. Тогда:
.
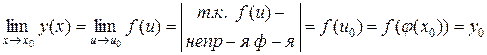Таким образом, получили: 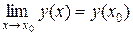, следовательно, функция 
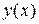непрерывна в точке .
§ 18. Свойства функций, непрерывных на отрезке 
Определение 1. Пусть функция определена на множестве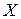 
. Наибольшим значением функции называется такое число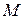 
, что для любого 
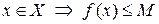и для любого 
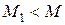существует 
: 
.
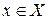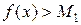Обозначение: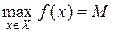 
.
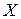Определение 2. Наименьшим значением функции на множестве называется такое число 
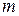, что для любого 
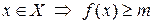и для любого 
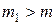существует : 
.
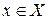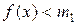Обозначение: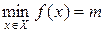 
.
Наибольшее и наименьшее значения могут не достигаться функцией.
Пример.
Рассмотрим функцию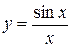 
на интервале 
.
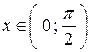Функция 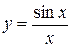убывает, 
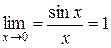, наименьшее значение 1.
Теорема 1. Пусть функция определена и непрерывна на отрезке 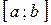. Тогда она достигает на этом отрезке своего наименьшего и своего наибольшего значения.
Теорема 2. Пусть функция непрерывна на отрезке 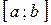и принимает различные по знаку значения на его концах, т.е. 
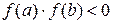. Тогда существует хотя бы одно 
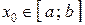такое, что 
.
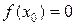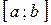Теорема 3 (о промежуточном значении). Пусть функция непрерывна на отрезке и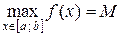 
, 
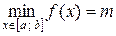. Тогда для любого числа 
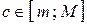существует 
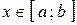такое, что 
.
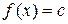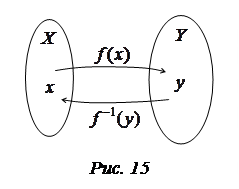Определение 3. Пусть дана функция 
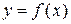. Тогда обратной функцией для называется функция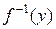 
: для любого 
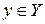выполняется 
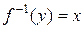, где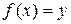 
(рис. 15).
Теорема 4. Пусть функция определена и непрерывна на отрезке 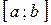и является на всем этом отрезке либо возрастающей функцией, либо убывающей. Тогда обратная функция 
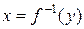будет непрерывной на отрезке 
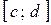, где 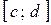– множество значений функции .
