Коллективные решения

Коллективные решения принимаются в результате голосования. Существует множество способов голосования. Вопросами принятия коллективных решений человечество интересуется уже давно. Одним из первых, кто заинтересовался системами голосования еще в XVIII веке, был французский ученый маркиз де Кондорсе. Он сформулировал принцип, позволяющий определять победителя в демократических выборах:

Каждый избиратель должен упорядочить всех кандидатов в порядке убывания предпочтений и побеждает тот кандидат, который является лучшим при сравнении один на один с любым другим кандидатом.

Однако, при использовании данной системы на практике, Кондорсе столкнулся с парадоксальным результатом, который получил название «парадокса Кондорсе». Рассмотрим его на примере.

Предположим, что в выборах участвуют 3 кандидата: А, В и С. Предпочтения 100 избирателей распределились следующим образом:

Предпочтения	Число голосов	Предпочтение	Число голосов
А→В→С		В→С→А
А→С→В		С→А→В
В→А→С		С→В→А

Рассмотрим пару А-В. За предпочтение А проголосовало 23+13+16=52 избирателя, за В: 7+22+19=48 избирателей, в этой паре победил А (обозначим это как А→В).

Рассмотрим пару А-С. За предпочтение А проголосовало 23+13+7=43 избирателя, за С: 22+16+19=57 избирателей, в этой паре победил С (обозначим это как С→А).

Рассмотрим пару В-С. За предпочтение В проголосовало 23+7+22=52 избирателя, за С: 13+16+19=48 избирателей, в этой паре победил В (обозначим это как В→С).

В результате получаем С→А→В→С, то есть С лучше А, который лучше В, но В оказывается лучше С! Очевидно, что данная система голосования не совершенна.

Одной из самых распространенных систем голосования в мире является система, основанная на правиле большинства голосов, когда победителем считается тот, кто наберет больше всего первых мест. В нашем примере победит А (36 первых мест), у В 29 голосов за первые места, у С – 35 голосов. Однако данный метод голосования учитывает лишь наилучшее предпочтение, что, очевидно, является его недостатком. Кроме того, известно множество примеров когда (чисто психологически) избиратель вместо того, чтобы участвовать в определении наилучшего из двух явных лидеров, противодействуя им обоим, выводит на первое место аутсайдера, который потом и является победителем.

В последние годы в России при выборах президента и главы местного самоуправления применяется двухуровневая система, в которой на первом этапе по большинству голосов определяются два лидера, а на втором этапе, из их парных сравнений определяется победитель. Эту систему также нельзя назвать совершенной, т.к. учитываются лишь наилучшие предпочтения избирателей и, как показано в предыдущем примере, при парном сравнении избирателей может оказаться необъективный парадоксальный результат.

Еще один метод голосования был предложен Бордом. Согласно методу Борда, победитель определяется исходя из количества набранных очков. Предположим, что в выборах участвуют n кандидатов. Кандидат, занявший по предпочтениям первое место у избирателя получает n -1 очко, за второе место n -2 очка и так далее, за предпоследнее место – 1 очко, за последнее – 0 очков. Покажем на примере, что данный метод также не лишен недостатков. Предположим, что распределение голосов имело следующий вид:

Предпочтения	Число голосов
А→В→С
В→С→А
А→С→В
С→В→А

Кандидат А по системе Борда набрал 14×2+13×0+18×2+15×0=64 очка, В набрал 14×1+9×2+18×0+19×1=51 очко, а С набрал 14×0+9×1+18×1+19×2=65 очков. Видно, что победил С, хотя большинство первых мест (32 из 60) получил А.

В последнее время, особенно в телевизионных играх и шоу, очень распространены системы голосования с выбыванием, когда в течении нескольких туров для каждого кандидата вычисляются количества последних мест для каждого кандидата в каждом туре и из числа кандидатов удаляется тот, кто набрал максимальное число последних мест. По такой системе, исходя из предыдущего примера, в первом туре кандидат А набрал 28 последних мест, В – 18 мест и С – 14 мест. В первом туре исключается А. Во втором туре (без учета А) у В имеется 19+18=37 последних мест, а у С – 14+9=23 мест, исключается В, выиграл С. Видно, что кандидат А, который имеет большинство первых мест, был исключен уже в первом туре, что подтверждает несовершенство и этой системы голосования.

На основании приведенных примеров можно сделать вывод, что ни одна из приведенных систем голосования не совершенна и результат принятия коллективного решения зависит от системы голосования. В середине прошлого века Эрроу сформулировал аксиомы, которым должна удовлетворять совершенная система голосования. Последователи Эрроу, изучающие методы принятия коллективных решений, практически доказали, что методов голосования, удовлетворяющих аксиомам Эрроу (и, соответственно, совершенных) при числе кандидатов больше двух не существует. Следовательно, на результат принятия коллективного решения значительное влияние оказывает система голосования. Поэтому, в реальных выборах, нужно однозначно оговаривать систему голосования с избирателями и другими участниками принятия решения.

Рассмотрим на примере результаты принятия коллективного решения разными методами голосования.

Пример.

В коллективных выборах участвуют 4 кандидата: А, B, C и D. Голоса 150 избирателей были распределены по следующим схемам предпочтений:

Предпочтения	Число голосов	Предпочтения	Число голосов
А®B®C®D		C®D®B®A
A®C®D®B		C®A®B®D
A®D®B®C		C®A®D®B
B®A®C®D		D®C®B®A
B®D®C®A		D®C®A®B
B®C®D®A		D®A®B®C

Рассмотрим методы определения победителя среди кандидатов по различным схемам голосования.

1. Выбор победителя по большинству первых мест в одном туре.

Кандидаты набрали голоса избирателей за первые места в количестве:

А: 13+8+15=36; B: 16+12+9=37; C: 4+23+11=38; D: 18+14+7=39.

Победил кандидат D.

2. Выбор победителя в двух турах - по большинству первых мест в первом туре, лучшие два выходят во второй тур и победитель определяется исходя из парных предпочтений.

Во второй тур вышли D (39 голосов) и C (38 голосов).

В паре C-D за C проголосовало 13+8+16+9+4+23+11=84 голоса, за D проголосовало 15+12+18+14+7=66 голоса, победил С.

3. Выбор победителя по системе Кондорсе, в результате парных сравнений кандидатов.

Рассмотрим число голосов для каждой пары кандидатов

Пара A-B. За А: 13+8+15+23+11+14+7=91. За В: 16+12+9+4+18=59, получаем А®В.

Пара А-С. За А: 13+8+15+16+7=59. За С: 12+9+4+23+11+18+14=91, получаем С®А.

Пара А-D. За А: 13+8+15+16+23+11=86. За D: 12+9+4+18+14+7=64, получаем А®D.

Пара В-С. За В: 13+15+16+12+9+7=72. За С: 8+4+23+11+18+14=78, получаем С®В.

Пара В-D. За В: 13+16+12+9+23=73. За D: 8+15+4+11+18+14+7=77, получаем D®B.

Пара С-D. За С: 13+8+16+9+4+23+11=84. За D: 15+12+18+14+7=66, получаем С®D.

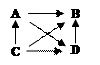Наглядно показать кто победил по методу Кондорсе поможет граф предпочтений, который представляет собой схему, состоящую из вершин, каждая из которых соответствует кандидату, и стрелок, определяющих предпочтения для каждой пары кандидатов:

Видно, что победил кандидат С, он оказался лучшим в парных сравнениях со всеми остальными кандидатами (на графе из вершины «С» выходят все стрелки). Худшим оказывается кандидат В (на графе в вершину «В» входят все стрелки).

Следует отметить, что могут быть ситуации, когда нет ни одного кандидата, победившего в парных сравнениях всех остальных. Такие варианты голосования иллюстрируют «парадокс Кондорсе».

4. Выберем победителя по системе Борда, когда за первое место набирается 3 очка, за второе – 2, за третье – 1 очко и за четвертое – 0.

Посчитаем очки, набранные кандидатами по этой системе.

Кандидат А набрал: 3×(13+8+15)+2×16+0×(12+9+4)+2×(23+11)+0×18+ +1×14+2×7=236 очков.

Кандидат В набрал: 2×13+0×8+1×15+3×(16+12+9)+1×(4+23)+0×11+ +1×18+0×14+1×7=204 очков

Кандидат С набрал: 1×13+2×8+0×15+1×(16+12)+2×9+3×(4+23+11)+ +2×(18+14)+0×7=253 очка.

Кандидат D набрал: 0×13+8×1+2×15+0×16+2×12+1×9+2×4+0×23+ +1×11+3×(18+14+7)=180 очков.

Видно, что по данной системе победил С, набравший большинство очков.

5. Выберем победителя по многотуровой системе, в которой на каждом туре отсеивается один, последний, кандидат.

Вычисляем количество последних мест для каждого кандидата в первом туре. Для А – 12+9+4+18=43 последних места, для В – 8+11+14=33 места, для С – 15+7=22 места, для D – 13+16+23=52 последних места. Видно, что наихудшим в первом туре оказался D, который набрал больше всего последних мест, поэтому исключаем именно его.

Во втором туре по исходной таблице вычисляем количество последних мест для участников А, В и С. При этом, в исходном раскладе голосов кандидата D не учитываем (то есть если в предпочтениях на последнем месте стоит кандидат D, то баллы за последнее место прибавляем предпоследнему кандидату). В результате во втором туре А набирает 12+9+4+18=43 последних места, В имеет 8+23+11+14=56 места, С набирает 13+15+16+7=51 последних места. Исключаем В.

В третьем туре, исходя их предпочтений пары А-С, выигрывает С, набрав 91 голос против 59.

Таким образом, результат голосования зависит от того, по какой системе оно производится.