Предельная теорема для суммарного потока

Предельная теорема для суммы нескольких потоков имеет такое же значение, как и центральная предельная теорема для суммы нескольких случайных величин. Центральная предельная теорема утверждает сходимость закона распределения суммы независимых случайных величин к нормальному закону при увеличении числа слагаемых. Предельная теорема для суммарного потока утверждает сходимость суммы независимых, ординарных, стационарных потоков к простейшему потоку. При этом условия, налагаемые на суммируемые потоки, приблизительно такие же, как и условия центральной предельной теоремы: складываемые потоки должны оказывать более или менее одинаково малое влияние на суммарный поток. Другими словами, среди суммируемых потоков не должно быть потоков с очень большой интенсивностью (по сравнению с суммарной интенсивностью всех остальных); интенсивности складываемых потоков не должны становиться по мере увеличения номера потока исчезающе малыми; кроме этого, должны быть наложены некоторые несуществующие ограничения на последействие внутри каждого потока. Здесь важно отметить, что сходимость суммарного потока к простейшему осуществляется очень быстро. Практически можно считать, что сложения четырех-пяти стационарных, ординарных, независимых потоков, сравнимых по интенсивности, достаточно для того, чтобы суммарный поток был близок к простейшему.

Остановимся подробнее на понятии «сложение» потоков. Сложение двух потоков П₁ и П₂ состоит в том, что все моменты появления событий в этих потоках относятся к одной оси t (рис. 2.6), на которой отмечаются моменты появления событий в суммарном потоке П = П₁ + П₂.

При сложении n потоков интенсивность суммарного потока определяется следующим образом:

,

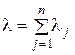где 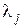– интенсивность j -го потока событий.

Таким образом, для выяснения всех свойств суммарного потока событий достаточно знать лишь интенсивности суммирующих потоков событий и практически не нужно знать внутреннюю структуру этих потоков.

Как указывалось выше, для сходимости суммарного потока событий к простейшему требуется взаимная независимость складываемых потоков. Поясним понятие независимости потоков на примере двух потоков. Рассмотрим участок времени t₁, наложенный на поток событий П₁. Участок t₁ может иметь произвольную длительность, и начало его может быть в произвольной точке t ₁ оси времени t (см. рис. 2.6).

Таким же образом выберем участок времени t₂ в потоке П₂. Случайное число событий в потоке П₁, наступающих на участке времени t₁, обозначим х ₁. Случайное число событий в потоке П₂, наступающих на участке времени t₂, обозначим х ₂. Потоки событий П₁ и П₂ называются независимыми, если случайные величины х ₁ и х ₂ независимы. Другими словами это можно сформулировать так: два потока называются независимыми, если число событий, попадающих на любой участок времени в первом потоке, не зависит от того, сколько событий попало на любой участок времени во втором потоке.

На практике часто потоки возникают в результате сложения не строго независимых, а слабо зависимых потоков событий. Исследования, проведенные методом статистических испытаний, показывают, что и в этом случае (при достаточном числе слагаемых) суммарный поток также оказывается близок к простейшему.

До сих пор рассматривалось сложение стационарных потоков событий. Оказывается, если складываемые потоки не стационарны, то предельное свойство также имеет место: получается суммарный поток, близкий к нестационарному пуассоновскому с интенсивностью

,

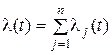где 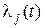– переменная интенсивность j -го потока.

При этом для любого момента времени t интенсивности всех потоков должны быть соизмеримы.

Из всего вышеизложенного следует, что многие потоки событий, возникающие на практике и фигурирующие в задачах массового обслуживания, можно приближенно считать пуассоновскими.

Например, поток космических частиц является практически пуассоновским, так как частицы порождаются очень большим числом звезд, испускающих эти частицы независимо друг от друга. Поток машин на загородном шоссе будет также практически пуассоновским потоком, так как он состоит из отдельных машин, выезжающих на шоссе с различных улиц и дорог. Поток самолетов, осуществляющих посадку на аэродром, также близок к пуассоновскому, несмотря на то, что его стремятся сделать строго регулярным (заранее планируют время приземления каждого самолета). Это объясняется тем, что самолеты прибывают к аэродрому не в строго заданное время (раньше или позже) и тем самым вносят элемент случайности в поток приземлений (каждый самолет независимо от других).

Заметим, что пуассоновский поток обладает устойчивостью, состоящей в том, что при суммировании независимых пуассоновских потоков получается снова пуассоновский поток, причем интенсивности складываемых потоков суммируются.