Как уже отмечалось, законы Ньютона справедливы только в инерциальных системах отсчета. Относительно всех инерциальных систем данное тело обладает одинаковым ускорением 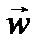 . Поскольку любаянеинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, ускорение тела в неинерциальной системе отсчета
. Поскольку любаянеинерциальная система отсчета движется относительно инерциальных систем с некоторым ускорением, ускорение тела в неинерциальной системе отсчета 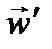 будет отлично от
будет отлично от 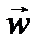 . Обозначим разность ускорений тела в инерциальной и неинерциальной системах символом
. Обозначим разность ускорений тела в инерциальной и неинерциальной системах символом 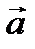 :
:
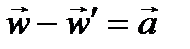 . (42)
. (42)
Если неинерциальная система движется относительно инерциальной поступательно, то 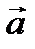 совпадает с ускорением неинерциальной системы отсчета. При вращательном движении различные точки неинерциальной системы имеют неодинаковое ускорение. В этом случае
совпадает с ускорением неинерциальной системы отсчета. При вращательном движении различные точки неинерциальной системы имеют неодинаковое ускорение. В этом случае 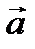 нельзя трактовать как ускорение, скоторым неинерциальная система движется относительно инерциальной.
нельзя трактовать как ускорение, скоторым неинерциальная система движется относительно инерциальной.
Пусть результирующаявсех сил, обусловленных действием на данное тело со стороны других тел, равна 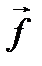 . Тогда согласно второму закону Ньютона
. Тогда согласно второму закону Ньютона
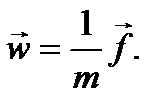
Ускорение же относительно в неинерциальной системы отсчета можно в соответствии с (42)представить и виде
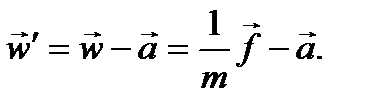
Таким образом, даже если результирующая всех сил, приложенных к телу, будет равна нулю, тело будет двигаться по отношению к неинерциальной системе отсчета с ускорением – 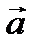 , т. е. так, как если бы на него действо вала сила, равная
, т. е. так, как если бы на него действо вала сила, равная 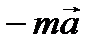 .
.
Следовательно, при описании движения в неинерциальных системах отсчета можно пользоваться уравнениями динамики, справедливыми только для инерциаль-ных систем, если наряду с силами, обусловленными воздействием тел друг на друга, учитывать так называемые силы инерции 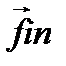 , которые следует полагать равными произведению массы тела на взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной системам отсчета:
, которые следует полагать равными произведению массы тела на взятую с обратным знаком разность его ускорений по отношению к инерциальной и неинерциальной системам отсчета:
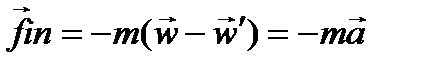 . (43)
. (43)
Тогда уравнение второго закона Ньютона в неинерциальной системе отсчета будет иметь вид
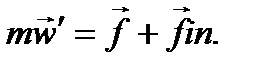 (44)
(44)
Поясним сказанное следующим примером. К кронштейну, закрепленному на тележке, подвешен на нити груз (рис. 15). Пока тележка покоится или движется без ускорения, нить расположена вертикально и сила тяжести 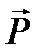 уравновешивается реакцией нити
уравновешивается реакцией нити 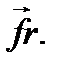 Теперь приведем тележку в поступательное движение с ускорением
Теперь приведем тележку в поступательное движение с ускорением 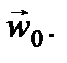 Нить отклонится от вертикали на такой угол, чтобы результирующая сил
Нить отклонится от вертикали на такой угол, чтобы результирующая сил 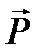 и
и 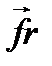 обеспечивала ускорение тела, равное
обеспечивала ускорение тела, равное 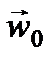 . Относительно системы отсчета, связанной с тележкой, тело покоится, несмотря на то, что результирующая сил
. Относительно системы отсчета, связанной с тележкой, тело покоится, несмотря на то, что результирующая сил 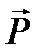 и
и 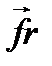 отлична от нуля. Отсутствие ускорения тела по отношению к этой системе отсчета можно формально объяснить тем, что, кроме сил
отлична от нуля. Отсутствие ускорения тела по отношению к этой системе отсчета можно формально объяснить тем, что, кроме сил 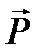 и
и 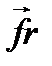 на тело действует еще и сила инерции
на тело действует еще и сила инерции
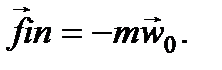 (45)
(45)
Введение сил инерции дает возможность описывать движение тел в любых (как инерциальных, так и неинерциальных) системах отсчета с помощью одних и тех же уравнений движения.
Следует отчетливо понимать, что силы инерции нельзя ставить в один ряд с такими силами, как упругие, гравитационные силы и силы трения, т. е. силами, обусловленными воздействием на тело со стороны других тел. Силы инерции обусловлены свойствами той системы отсчета, в которой рассматриваются механические явления. В этом смысле их можно назвать фиктивными силами.
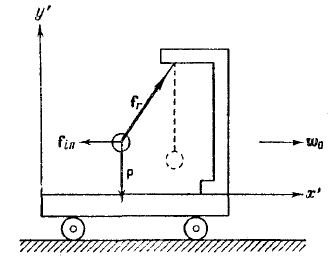
Рис. 15.
Силы инерции в системе отсчета, движущейся с ускорением
 2015-02-14
2015-02-14 922
922







