Определение непрерывности функции

Непрерывность функции

Функция 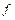: 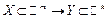называется непрерывной в точке 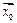, если выполнено одно из условий:

1) (на языке окрестностей)

для 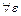- окрестности 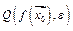значения 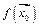функции в точке 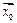найдется такая 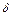-окрестность 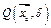этой точки, образ которой при отображении 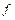содержится в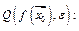

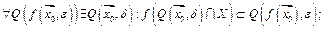
2) (на языке модулей)

для 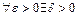такое, что лишь только 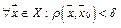, так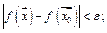

3) (в предельной точке)

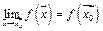, где 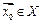- предельная точка множества .

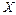Определения 1 и 2 не связывают понятие непрерывности с понятием предела и остаются годными и для изолированной точки 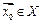, в которой функция непрерывна.

Для непрерывной в предельной точке 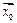функции можно записать:

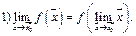
2)

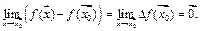
Справедливы следующие теоремы:

Теорема о покоординатной непрерывности:

Для того чтобы функция 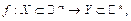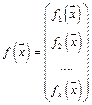была непрерывной в точке 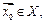необходимо и достаточно, чтобы в точке 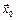были непрерывны компоненты функции .

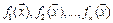Теорема о действиях над непрерывными функциями.

Если функции 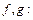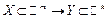непрерывны в точке 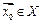,то

1) для 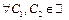функция 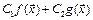непрерывна в точке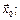

2) скалярное произведение 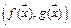непрерывно в точке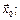

3) если 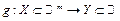непрерывна в точке 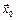и 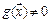, то функция 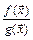непрерывна в точке .

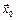Теорема о непрерывности сложной функции.

Пусть функция 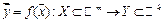непрерывна в точке 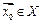а функция 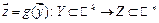непрерывна в точке 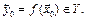Тогда композиция 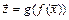непрерывна в точке .

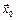Для функции одной переменой вводится понятие односторонней непрерывности