Типы преобразователей сигналов:
1. Ключевой квантователь сигналов;

Математический аппарат исследования дискретных САУ основывается на замене последовательности реальных импульсов последовательностью идеальных импульсов и формирователем сигналов при выполнении условий:
1. Продолжительность замыкания ключа квантователя значительно меньше такта квантования (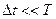 );
);
2. Период квантования T=const;
3. Сопротивление ключа квантователя в замкнутом состоянии равно нулю, в разомкнутом 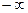 ;
;
4. Сигнал с выхода квантователя подается на линейную (в ней выполняется принцип суперпозиции) реализуемую непрерывную часть системы;
5. Если система содержит несколько квантователей, то считаем квантователи одинаковыми по характеристикам и синхронно работающими.
Аналоговая часть системы воспринимает входное воздействие как импульсное, если длительность импульса значительно меньше эквивалентной инерционности аналогового устройства W(p); на выходе системы – реакция на площадь входного реального импульса (аналогично действию импульса силы на твердое тело в механике).
Аналитическое выражение последовательности импульсов 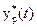 , имеющих площадь
, имеющих площадь 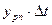 , имеет вид
, имеет вид
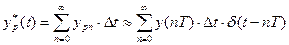 при модуляции первого рода, где
при модуляции первого рода, где
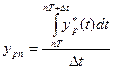 - эквивалентная амплитуда импульса в n-ый момент замыкания ключа;
- эквивалентная амплитуда импульса в n-ый момент замыкания ключа;
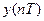 - амплитуда импульса в начальный момент n-го замыкания ключа;
- амплитуда импульса в начальный момент n-го замыкания ключа;
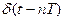 - смещенная дельта-функция, существующая только в моменты времени
- смещенная дельта-функция, существующая только в моменты времени 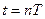 и равная нулю при всех других значениях t.
и равная нулю при всех других значениях t.
Идеальный импульсный элемент можно рассматривать как импульсный модулятор с несущей в виде последовательности мгновенных единичных импульсов
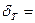
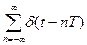
и огибающей в виде входного непрерывного сигнала u(t), т.е.
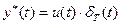 .
.
Функцию 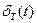 называют функцией единичных импульсов и широко используют при исследовании импульсных систем.
называют функцией единичных импульсов и широко используют при исследовании импульсных систем.
C целью упрощения анализа заменим реальный модулятор идеальным импульсным элементом и формирователем импульсов:
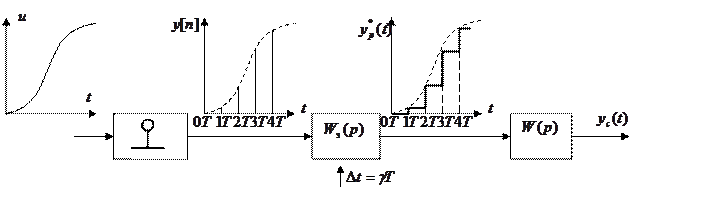
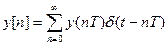 - решетчатая функция амплитудно-импульсного модулятора-
- решетчатая функция амплитудно-импульсного модулятора-
уравнение амплитудно-импульсного модулятора во временном
пространстве.
Wэ(p) – экстраполятор нулевого порядка, 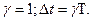
Определение: “Решетчатая функция- выходная временная функция элемента САУ, значения которой определены в дискретные моменты времени t=nT (n -числа натурального ряда, T - период квантования) путем повторных равноотстоящих измерений входного воздействия и обозначаемая y[nT] (сокращенно y[n])”.
Дискреты (ординаты входных воздействий) могут определяться также и для смещенных моментов времени 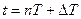 , где
, где 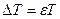 - константа может быть положительной или отрицательной величиной при условии
- константа может быть положительной или отрицательной величиной при условии 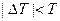 ,
, 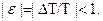
Решетчатая функция в этом случае называется смещенной и обозначается 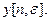
В дальнейшем будем считать параметр 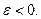 Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.
Непрерывные функции, совпадающие с заданными дискретами, называются огибающими решетчатой функции.
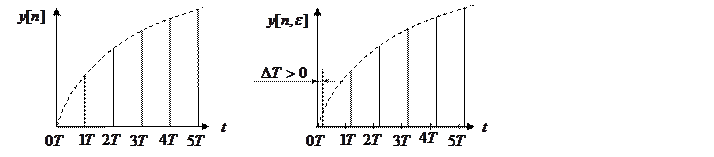
2. Аналого-цифровой модулятор
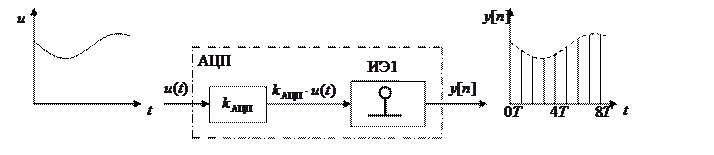
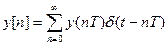 , где
, где 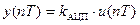
ИЭ1 – идеальный импульсный элемент первого рода. Вид модуляции: амплитудно-кодовая.
3. Цифро-аналоговый демодулятор

ИЭ2 – идеальный импульсный элемент второго рода. Вид модуляции: амплитудно-импульсная.
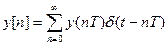 , где
, где 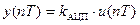
 2015-02-04
2015-02-04 577
577








