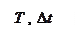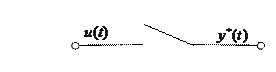
2015-02-04
536
 |
Периодическая последовательность δ-импульсов может быть представлена в виде комплексного ряда Фурье
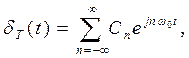
где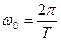 
-частота квантования во времени, n-номер гармоники (n=0,1,2,…), 
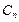-коэффициенты ряда Фурье:
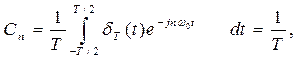
Тогда
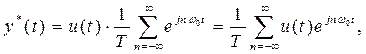
преобразование Лапласа этого уравнения дает
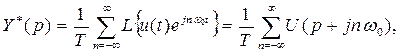
преобразование Фурье имеет вид
,
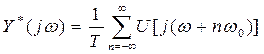которое означает, что частотный спектр на выходе идеального импульсного элемента представляет собой сумму частотных спектров непрерывного сигнала на входе элемента, смещенных по оси частот на величину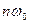 
.
Вообще, периодические временные функции имеют дискретные частотные спектры, а дискретные временные функции – периодические частотные спектры.
 |
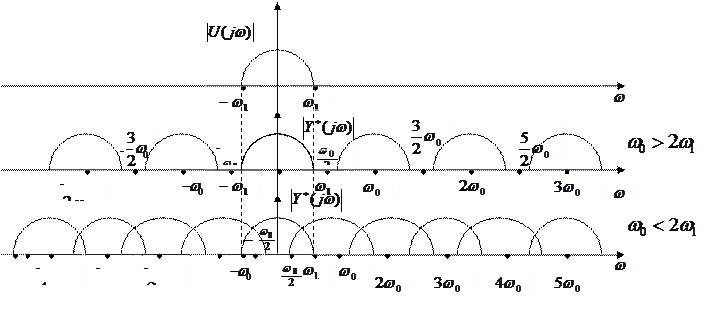
Частотные спектры входного непрерывного сигнала и выходного сигнала импульсного элемента пр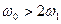и 
и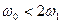 
Расчет цифровых САУ следует вести так, чтобы выполнялись условия импульсной теоремы Котельникова-Шеннона:
“Для того чтобы передаваемая в виде импульсов информация могла быть воспроизведена без существенных искажений, наивысшая частота гармоник со значимыми амплитудами в спектре входного сигнала не должна превышать 1/2 частоты следования импульсов”.
|
|
|
При достаточно большой частоте импульсов образующих выходной сигнал импульсного элемента, непрерывная часть системы реагирует только на низкочастотную составляющую сигнала, несущую информацию о непрерывном сигнале на входе импульсного элемента. Дискретность работы импульсного элемента обусловливает, лишь в качестве побочного явления возникновение на выходе системы высокочастотной составляющей в виде помехи, частотный спектр которой кратен частоте импульсного элемента.
Условие допустимости сведения импульсной системы к непрерывной:
,
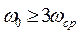где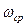 
- частота среза непрерывной части системы,
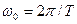- частота квантования во времени.
