Z–преобразование вытекает из дискретного преобразования Лапласа путем введения новой переменной 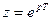 .
.
Z–преобразование есть изображение несмещенной или смещенной решетчатых функций, определяемое формулами
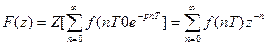
 ,
, 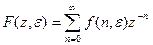 .
.
Способы перехода от непрерывных моделей к дискретным:
1. Применение Z – преобразования к решетчатой импульсной переходной функции со следующей цепочкой переходов (точный способ):
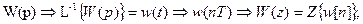
2. Замена производных дифференциального уравнения, описывающего объект, приближенными разностями:
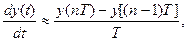
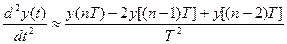 и т. д.;
и т. д.;
Данный способ дает приемлемую точность только при малых T.
3. Приближенный способ, предложенный А.Тастеным и называемый билинейным преобразованием, состоит в замене оператора p в передаточной функции соотношением
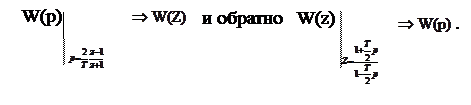
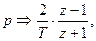 т.е.
т.е.
Если для данной решетчатой функции f[n] существует такое положительное число R, что при |z|>R ряд 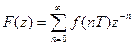 (5)
(5)
сходится, то r=1/R называют радиусом сходимости.
Функция 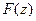 внутри круга сходимости (т.е. круга в плоскости z с центром в начале координат и радиусом равным r) будет аналитической функцией, а ряд (5) будет рядом Лорана. Коэффициенты ряда f[nT] выражаются через
внутри круга сходимости (т.е. круга в плоскости z с центром в начале координат и радиусом равным r) будет аналитической функцией, а ряд (5) будет рядом Лорана. Коэффициенты ряда f[nT] выражаются через 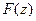 следующим образом:
следующим образом:
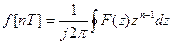 .
.
Формулы преобразования могут быть записаны и для непрерывной производящей функции в виде
F(z)=Z{f(t)}, t=nT, n=0,1,2,….
В рассматриваемом пространстве введена единичная импульсная решетчатая функция 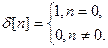
Эта функция играет в дискретных системах такую же важную роль, как d - функция (функция Дирака) в непрерывных системах.
Основные свойства и теоремы Z-преобразования
Изображение линейной комбинации решетчатых функций равно той же линейной комбинации их изображений.
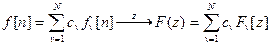 .
.
2. Теорема запаздывания.
Рассмотрим решетчатую функцию f[n-m], сдвинутую вправо (запаздывающую) на целое число тактов m. Если обозначить n-m=r, то
Z{f[n-m]}= 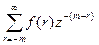 =
= 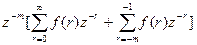 =
= 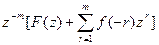 .
.
Если исходная решетчатая функция f[n] равна нулю при отрицательных значениях аргумента, то Z{f[n-m]}= 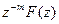 .
. 
Сдвиг по временной области.
Если 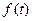 имеет z -преобразование
имеет z -преобразование 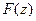 , то
, то
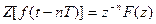 ,
,
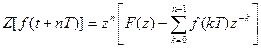 ,
,
где n – положительное целое число.
Доказательство.
По определению 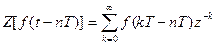 ,
,
что может быть записано как
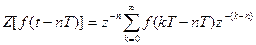 .
.
Предполагая, что 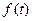 равно нулю при t < 0, получим последнее выражение в виде
равно нулю при t < 0, получим последнее выражение в виде
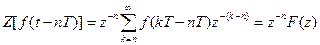 .
.
Для доказательства второго равенства запишем:
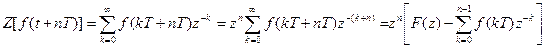 .
.
3. Изображение разностей.
Для первой обратной разности
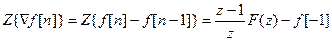 .
.
Если для отрицательных аргументов решетчатая функция тождественно равно нулю, то 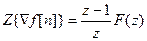 .
.
Для k-й обратной разности при f[n]º0 для n<0
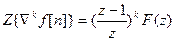 ,
,
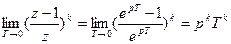 .
.
Определение обратной разности и неполной суммы (или прямой разности и полной суммы) решетчатой функции являются обратными операциями. Роль оператора, аналогичного оператору p=c+jω в непрерывных системах, в первом случае играет оператор (z-1)z-1, а во втором случае – оператор (z-1). В случае перехода к пределу при T®0 обе пары операций над решетчатыми функциями сливаются и превращаются в операции дифференцирования и интегрирования непрерывной функции.
4. Теорема о конечном значении решетчатой функции.
«Если функция f(t) имеет z – преобразование F(z) и если функция 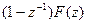 не имеет полюсов на окружности единичного радиуса |z|= 1 и вне её на z – плоскости, то при исследовании систем управления, в которых используются обратные разности, справедливо равенство:
не имеет полюсов на окружности единичного радиуса |z|= 1 и вне её на z – плоскости, то при исследовании систем управления, в которых используются обратные разности, справедливо равенство:
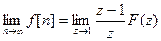 ».
».
Доказательство.
Рассмотрим два ряда с конечным числом членов:
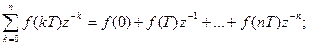
полагая, что f(t)= 0 при t< 0 и, следовательно, f(-T) равно нулю, запишем выражение второго
ряда
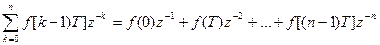 .
.
Сравнивая эти выражения, видим, что второй ряд может быть записан как
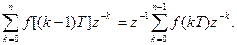
Определим в пределе при 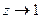 разность между выражениями:
разность между выражениями:
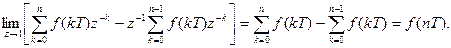
В последнем выражении возьмём предел при 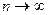 , тогда
, тогда
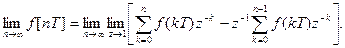
Меняя порядок перехода к пределу в последнем выражении и учитывая, что
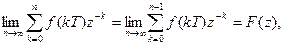
получим 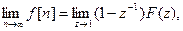
что и является доказательством теоремы о конечном значении.
Пример. Конечное значение единичной функции 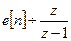 определяется следующим образом:
определяется следующим образом:

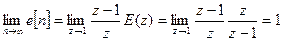 .
.
5. Теорема о начальном значении решетчатой функции.
«Если функция f(t) имеет z – преобразование F(z) и если существует предел 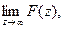 то
то
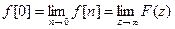 ».
».
Доказательство.
По определению F(z) можно представить в виде
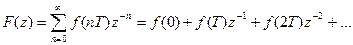 .
.
Возьмём предел от каждой части последнего выражения и, учитывая, что z стремится к бесконечности, получим
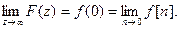
Пример. 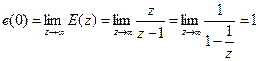 .
.
6. Разложение в ряд Лорана (ряд по убывающим степеням z).
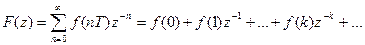 .
.
Разложив любым способом изображение F(z) в ряд Лорана:
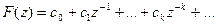 , и, сравнивая два ряда между собой, можно установить, что
, и, сравнивая два ряда между собой, можно установить, что
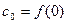 ,
, 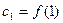 ,
, 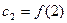 ,…,
,…, 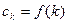 и т.д.
и т.д.
7. Решение разностных уравнений.
Более удобны для решения разностные уравнения вида
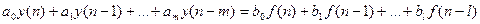
с начальными условиями 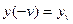 ,
, 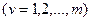 .
.
Изображение решетчатой функции y[n-m], запаздывающей на m тактов, будет 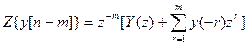 .
.
Подобные зависимости могут быть записаны для запаздывания на (m-1), (m-2),…, 1 тактов.
В случае нулевых начальных условий 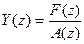 .
.
Если предположить, что решетчатая функция y[n] тождественно равна нулю при n < 0 и, кроме того, функция f[n] в правой части прикладывается в момент времени n=0, то переход к изображениям дает
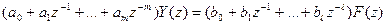 .
.
Изображение искомой решетчатой функции можно представить в виде
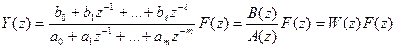 ,
,
где W(z) - дискретная передаточная функция.
Пример 1.
Определить z - изображение единичной ступенчатой решетчатой функции ed[n] при T=1c.
ed(t) – производящая функция, преобразование по Лапласу которой L{ed(t)}= 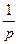 .
.
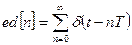 ;
; 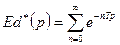 ;
; 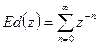 .
.
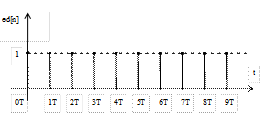 Используем формулу суммирования убывающей геометрической прогрессии
Используем формулу суммирования убывающей геометрической прогрессии
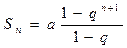 ,
,
где 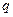 - знаменатель прогрессии,
- знаменатель прогрессии,
тогда 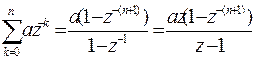 .
.
Для бесконечно убывающей прогрессии n®¥,
тогда 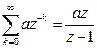 . Знаменатель прогрессии
. Знаменатель прогрессии 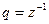 .
.
Тогда для |z|>1 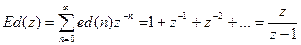 .
.
Пример 2. Задана решетчатая экспонента 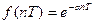 , где a - постоянная, в общем случае комплексная величина, T=1c.
, где a - постоянная, в общем случае комплексная величина, T=1c.
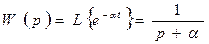 ;
;
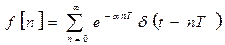 ;
;
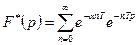 ;
;
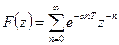 ;
;
знаменатель прогрессии q=z-1 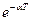 .
.
Для |z| > e-αT
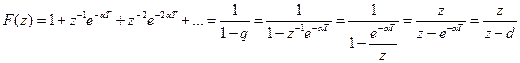 , где d=e-αT.
, где d=e-αT.
| NN n. n. | w (t) | w (nT) | W(p) | W(z) |
| . . . |   . . . . . . | 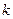 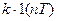 . . . . . . | 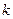 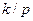 . . . . . . | 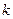 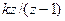 . . . . . . |
 2015-02-04
2015-02-04 4438
4438