1. Метод прямого расчёта 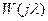 и построение по ней ЛПЧХ.
и построение по ней ЛПЧХ.
Для построения ЛПЧХ разомкнутой ЦАС определяют дискретную передаточную функцию разомкнутой системы, затем путем подстановки
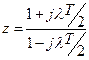
получают дискретную частотную передаточную функцию разомкнутой цифровой системы 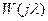 . Порядок построения ЛЧХ цифровых систем по дискретным частотным передаточным функциям такой же, как и для непрерывных систем.
. Порядок построения ЛЧХ цифровых систем по дискретным частотным передаточным функциям такой же, как и для непрерывных систем.
Такой путь определения ЛПЧХ, как правило, ведет к громоздким и трудоемким построениям и промежуточным вычислениям, что связано с утратой основного достоинства метода – простоты и наглядности использования ЛЧХ.
Поэтому построение ЛПЧХ цифровых систем проводят обычно приближенными способами. Применимость этих способов зависит от вида передаточных функций непрерывной части САУ правее частоты 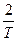 , наличия колебательных, консервативных и неминимально-фазовых звеньев, а также расположения их сопрягающих и резонансных частот относительно частоты
, наличия колебательных, консервативных и неминимально-фазовых звеньев, а также расположения их сопрягающих и резонансных частот относительно частоты 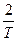 , порядка экстраполятора и вида
, порядка экстраполятора и вида 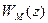 . Обычно используют или метод ограничений, или метод упрощенного расчета дискретной ЛЧХ в области высоких частот.
. Обычно используют или метод ограничений, или метод упрощенного расчета дискретной ЛЧХ в области высоких частот.
2. Метод ограничений.
ЛПЧХ целесообразно строить раздельно для области низких частот (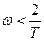 ) и для области высоких частот (
) и для области высоких частот (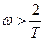 ).
).
В методе ограничений в области низких частот (левее частоты 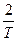 ) ЛЧХ дискретной частотной передаточной функции совпадает с ЛЧХ непрерывной части ЦАС, если
) ЛЧХ дискретной частотной передаточной функции совпадает с ЛЧХ непрерывной части ЦАС, если 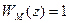 , а передаточные коэффициенты преобразователей приведены к передаточной функции непрерывной части системы.
, а передаточные коэффициенты преобразователей приведены к передаточной функции непрерывной части системы.
Если передаточная функция непрерывной части имеет вид
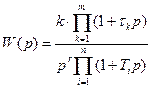 ,
,
где постоянные времени 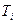 делятся на две группы: к первой группе (
делятся на две группы: к первой группе (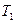 ,
, 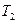 , …,
, …, 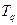 ) отнесем те из них, которым соответствуют сопрягающие частоты меньше
) отнесем те из них, которым соответствуют сопрягающие частоты меньше 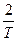 (большие постоянные времени), они участвуют в формировании низкочастотной части логарифмических характеристик; ко второй группе (
(большие постоянные времени), они участвуют в формировании низкочастотной части логарифмических характеристик; ко второй группе (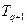 ,
, 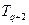 , …,
, …, 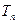 ) отнесем постоянные времени, которым соответствуют сопрягающие частоты больше чем
) отнесем постоянные времени, которым соответствуют сопрягающие частоты больше чем 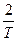 (малые постоянные времени). Постоянным времени
(малые постоянные времени). Постоянным времени 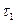 ,
, 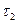 , …,
, …, 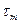 соответствуют сопрягающие частоты, меньшие частоты
соответствуют сопрягающие частоты, меньшие частоты 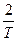 , то при пересечении ЛАЧХ САУ вертикальной прямой
, то при пересечении ЛАЧХ САУ вертикальной прямой 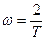 асимптотой с наклоном –20 дБ/дек дискретная частотная передаточная функция имеет вид
асимптотой с наклоном –20 дБ/дек дискретная частотная передаточная функция имеет вид
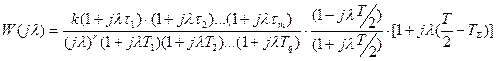 ,
,
где 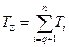 ;
;
при пересечении вертикальной линии 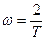 асимптотической ЛАЧХ непрерывной части системы с наклоном –40 дБ/дек
асимптотической ЛАЧХ непрерывной части системы с наклоном –40 дБ/дек
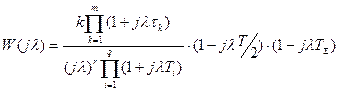 .
.
3.Метод упрощенного расчета.
Этот метод используют, например, когда в области частот 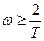 передаточную функцию непрерывной части исходной системы можно аппроксимировать выражением, для которого либо известна
передаточную функцию непрерывной части исходной системы можно аппроксимировать выражением, для которого либо известна 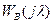 , либо может быть легко определена.
, либо может быть легко определена.
Например, если
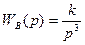 , где
, где 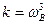 ,
,
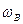 - частота, определяемая точкой пересечения асимптоты, имеющей наклон –60 дБ/дек с осью частот (эта асимптота проходит через точку сопряжения с низкочастотной частью ЛАЧХ на линии
- частота, определяемая точкой пересечения асимптоты, имеющей наклон –60 дБ/дек с осью частот (эта асимптота проходит через точку сопряжения с низкочастотной частью ЛАЧХ на линии 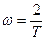 ), то построение псевдочастотной ЛЧХ производится по дискретной частотной передаточной функции:
), то построение псевдочастотной ЛЧХ производится по дискретной частотной передаточной функции:
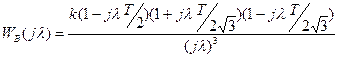 .
.
 2015-02-04
2015-02-04 865
865








