2015-02-04
895
В общем случае переходный процесс в линейной импульсной системе протекает неограниченно долго. Однако в отличие от непрерывных систем, здесь возможно создание условий, при которых длительность переходных процессов при произвольных воздействиях оказывается конечной. В таких системах, начиная с некоторого момента времени, импульсная характеристика тождественно равна нулю:
w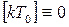 
при 
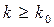, (1)
т.е. затухает для дискретных значений за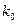 
периодов дискретности.
Учитывая связь между решетчатой весовой функцией цифровой системыи её дискретной передаточной функцией в виде
,
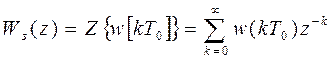получаем, что ДПФ цифровой системы, для которой справедливо условие (1), должна удовлетворять равенству
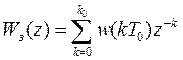. (2)
В общем случае дискретная передаточная функция замкнутой цифровой системы имеет вид отношения двух многочленов:
, 
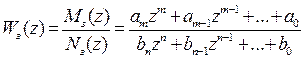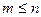. (3)
Сравнивая правые части (2) и (3), замечаем, что они могут быть тождественны лишь тогда, когда дробь в правой части равенства (3) превратится в многочлен. Но это может иметь место лишь тогда, когда
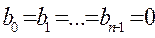, (4)
т.е. 
, 
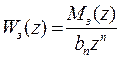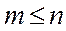. (5)
Действительно, при выполнении условий (4) из (5) получаем при учете (2):
,
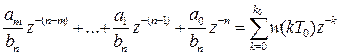откуда следует, что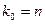 
.
Таким образом, при выполнении условий (4) весовая функция цифровой системы (ее дискретные значения) затухает за время, равно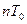е 
, где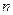 
-порядок полинома в знаменателе передаточной функции 
.
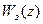Пример 1
Для цифровой системы определить условия, при которых переходный поцесс заканчивается за конечное число периодов дискретности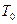 
.
Случай 1: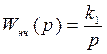 
, 
.
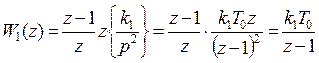Дискретная передаточная функция замкнутой системы имеет вид
.
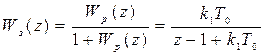Для того чтобы переходный процесс заканчивался за время 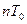(здесь 
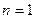), необходимо, чтобы полюс 
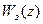был равен нулю. Это условие выполняется в том случае, если 
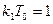, т.е. при выборе 
.
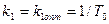Случай 2: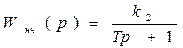 
, 
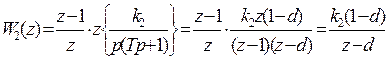, где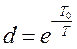 
.
Дискретная передаточная функция замкнутой системы имеет вид
.
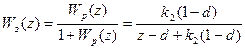Аналогично предыдущему случаю получаем, что переходный процесс в такой системе будет заканчиваться за один период дискретности при условии, если
,
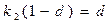т.е. при выборе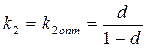 
.
Рассмотренные в примере простейшие импульсные системы отличает возможность достижения конечной длительности переходных процессов только за счет изменения параметров системы без изменения её структуры. В более общем случае для реализации условий (4) требуется введение в импульсную систему дополнительных корректирующих звеньев.
Рассмотрим включение корректирующего цифрового устройства последовательно в канал рассогласования системы.
Предположим, что мы хотим реализовать желаемую передаточную функцию замкнутой цифровой системы, удовлетворяющую условию (4), т.е. имеющую вид
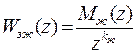, (6)
где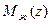 
-некоторый многочлен по 
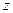степени 
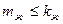(условие физической реализуемости передаточной функции).
Передаточная функция замкнутой цифровой системы с последовательным дискретным корректирующим устройством определяется выражением
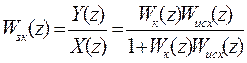, (7)
где 
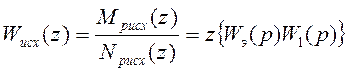(8)
- передаточная функция исходной (нескорректированной) системы в разомкнутом состоянии.
Подставив в (7)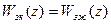 
и разрешив это уравнение относительно 
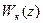, получим с учетом (6) необходимую передаточную функцию фильтра коррекции
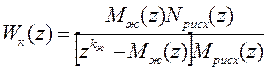, (9)
где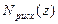 
, 
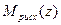- многочлены по 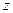степен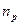и 
и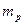 
соответственно, причем 
.
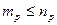Поскольку в числителе дроби (9) степень многочлена равна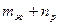 
, а в знаменателе 
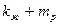, то из условия физической реализуемости 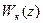следует, что желаемое число 
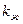периодов 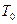затухания переходных процессов в системе должно удовлетворять условию
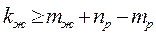. (10)
Минимальное число периодов затухания переходного процесса при неизменяемой части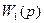 
из (10) равно
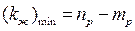, (11)
что соответствует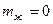 
, т.е. выбору в числителе (6) многочлена 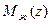нулевой степени или
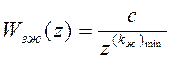. (12)
Подставив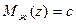 
в (9), получим соответствующую передаточную функцию фильтра коррекции
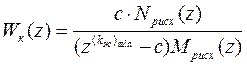. (13)
Свобода выбора коэффициента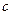 
в (12) может быть использована для придания системе некоторых добавочных полезных свойств. Например, если потребовать чтобы система помимо конечной длительности переходных процессов имела астатизм по управляющему воздействию 
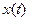, т.е.
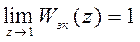
необходимо, чтобы коэффициент 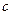в (12), (13) был выбран равным единице.
Пример 2
Для цифровой системы определить передаточную функцию 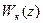, обеспечивающую минимальное конечное время затухания переходного процесса и нулевую установившуюся ошибку при скачкообразном входном воздействии,
.
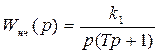Дискретная передаточная функция исходной (нескорректированной) системы в разомкнутом состоянии равна
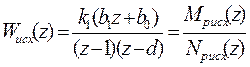, (14)
где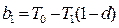 
, 
, 
.
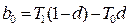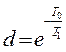Учитывая, что степени многочленов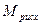 
и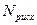 
в (14) соответственно равны 
, 
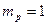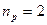, из (11) определяем 
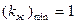, т.е.передаточную функцию 
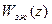замкнутой скорректированной системы принимаем в виде (с учетом (12), положив 
) 
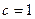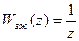. Тогда, используя (13), находим искомую передаточную функцию корректирующего дискретного фильтра
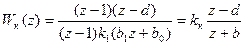, (15)
где обозначено: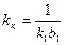 
, 
.
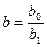При исследовании поведения цифровой системы с передаточной функцией дискретного фильтра коррекции, определяемой выражениями (9), (13) или (15) в промежутках между моментами замыкания импульсного элемента может оказаться, что в действительности в ней имют место скрытые колебания выходной величины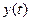 
в промежутках между моментами 
, 
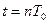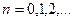, при 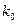в (1) равном двум. Появление подобных колебаний физически объясняется тем, что дискретный фильтр
а) б)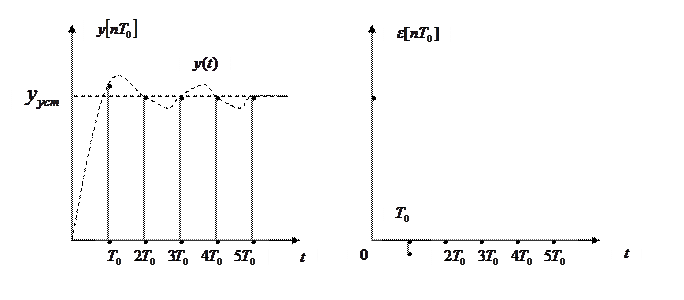 
коррекции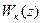 
даже после того как исчезли импульсы на его входе (на рис. б) это соответствует 
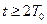) продолжает формировать импульсы на выходе. Удовлетворение требованию отсутствия скрытых колебаний приводит к увеличению числа периодов затухания переходного процесса.
