Опр: Квадратная матрица А называется невырожденной, если ее определитель не равен нулю, т.е. det A 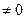
Опр: Матрицей, обратной к матрице А называется такая матрица 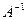 , которая удовлетворяет условиям:
, которая удовлетворяет условиям: 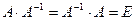 .
.
Все матрицы: А, 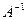 и Е имеют один и тот же порядок.
и Е имеют один и тот же порядок.
Всякая невырожденная матрица имеет обратную, которая может быть найдена по формуле: 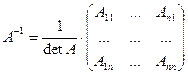 , где
, где 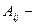 алгебраическое дополнение элемента
алгебраическое дополнение элемента 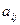 . Распишем последовательность нахождения обратной матрицы:
. Распишем последовательность нахождения обратной матрицы:
Правило вычисления обратной матрицы:
1. Вычислить определитель матрицы detA (detA 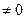 ,в противном случае обратная не существует.)
,в противном случае обратная не существует.)
2. Составить матрицу из алгебраических дополнений элементов: 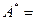
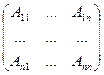
3. Каждый элемент полученной матрицы разделить на определитель: 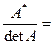
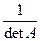
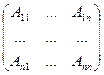
4. Транспонировать полученную матрицу: 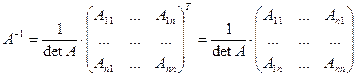
5. Результат проверить, умножив А на 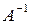 .
.
Пример: Для матрицы А= 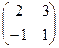 найти обратную.
найти обратную.
Решение:
1. Находим detA= 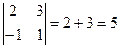
2. Составляем матрицу 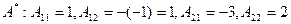 , поэтому
, поэтому 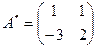
3. Делим элементы на определитель: 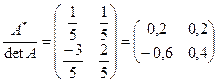
4. Транспонируем полученную матрицу: 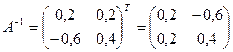
5. Проверка: 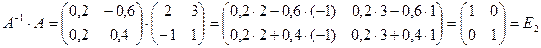
Ответ: 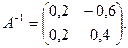
Пример: Для матрицы А= 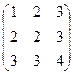 найти обратную.
найти обратную.
|
|
|
Решение:
Находим detA= 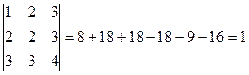
Составляем матрицу
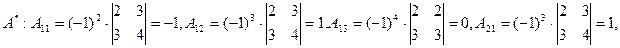
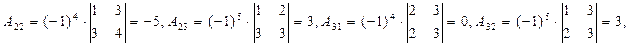
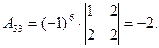 поэтому
поэтому 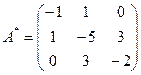
Делим элементы на определитель: 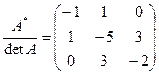
Транспонируем полученную матрицу: 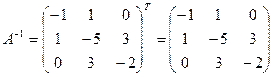
Проверка: 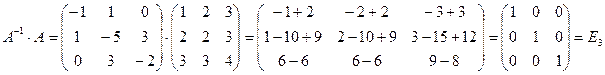
Ответ: 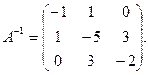
 2015-02-18
2015-02-18 388
388








