1. Прямой ход метода Гаусса: выписывается расширенная матрица системы(справа к матрице системы приписывается столбец свободных переменных)
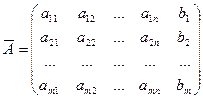 ,
,
применяем элементарные преобразования над строками для приведения матрицы к ступенчатому виду:
· строки можно переставлят местами;
· строку можно умножать на любое число, не равное нулю;
· к строке можно поэлементно прибавлять другую строку, умноженную на ненулевое число.
1-й этап:
Считая элемент 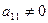 (в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме
(в противном случае переставляем местами строки), обнулим все элементы первого столбца кроме 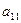 .
.
Для этого ко второй строке прибавим первую строку, умноженную на 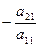 .
.
К третьей строке прибавим вторую, умноженную на 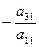 и т.д.
и т.д.
Получим преобразованную матрицу:
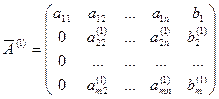 , где
, где 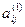 и
и 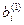 - преобразованные коэффициенты матрицы.
- преобразованные коэффициенты матрицы.
2-й этап:
Считая 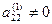 , обнулим все коэффициенты второго столбца, кроме
, обнулим все коэффициенты второго столбца, кроме 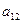 и
и 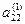 , для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент.
, для чего к каждой строке прибавляем вторую строку, умноженную на соответствующий коэффициент.
Если в процессе приведения появляется нулевая строка, ее выбрасываем. Если появляется строка, все коэффициенты которой нули, а последний 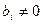 , то система несовместна.
, то система несовместна.
Обратный ход метода Гаусса: По виду ступенчатой матрицы: 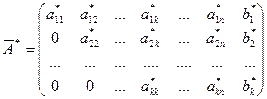 восстановить систему:
восстановить систему: 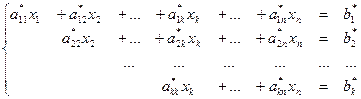 ,
,
Если число оставшихся уравнений и число переменных совпадает, то система имеет единственное решение. Если же переменных больше, чем уравнений, то переменные, вышедшие на диагональ называются главными, или зависимыми, а переменные не вышедшие на диагональ свободными. Свободные переменные необходимо перенести в правую часть уравнения и начиная с последнего уравнения выразить главную переменную 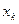 ,подставить в предпоследнее, из которого выразить
,подставить в предпоследнее, из которого выразить 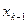 , и т.д., из первого уравнения выразить
, и т.д., из первого уравнения выразить 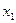 . В этом случае система имеет множество решений. Свободные переменные могут приобретать любые значения, и через них выражаются значения зависимых переменных.
. В этом случае система имеет множество решений. Свободные переменные могут приобретать любые значения, и через них выражаются значения зависимых переменных.
Пример 6: Решить систему методом Гаусса:
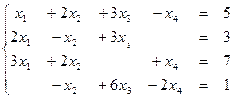
Решение: Выпишем расширенную матрицу системы и приведем ее к верхнетреугольному виду:
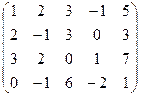
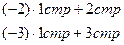
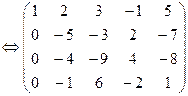
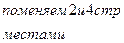
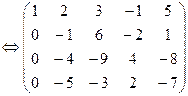
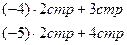
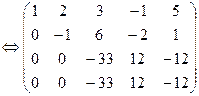
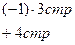
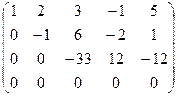
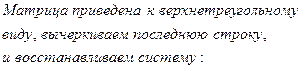
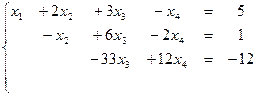
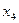 является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
является свободной переменной, т.к. не вышла на диагональ, переносим ее вправо. Система имеет бесконечное множество решений.
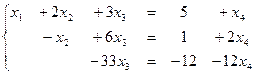
Из последнего уравнения выражаем 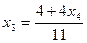
Из второго уравнения выражаем 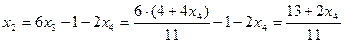
Из первого уравнения выражаем 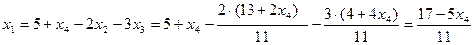
Выпишем общее решение системы: 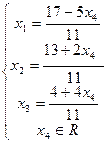
Ответ: Система имеет множество решений, общее решение системы:
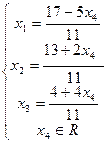
 2015-02-18
2015-02-18 649
649








