Система линейных уравнений называется однородной, если правые части уравнений равны нулю:
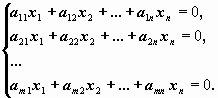
Матричный вид однородной системы: Ax=0.
Однородная система всегда совместна, поскольку любая однородная линейная система имеет по крайней мере одно решение:
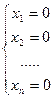
Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной. Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называется нетривиально совместной.
Доказано, что при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю. Линейная комбинация решений однородной системы также является решением этой системы.
Пример: Исследовать однородную систему на совместность, найти решения: 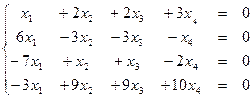
Решение: Расширенную матрицу системы приведем к ступенчатому виду: 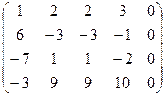
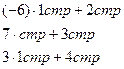
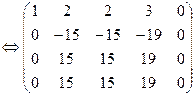
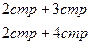
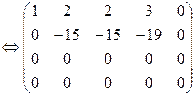
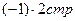
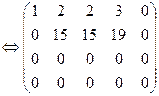 восстановим систему:
восстановим систему:
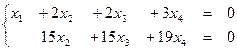
Система имеет множество решений. 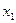 и
и 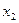 главные переменные,
главные переменные, 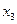 и
и 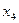 свободные переменные. Перенесем свободные переменные в правые части уравнений.
свободные переменные. Перенесем свободные переменные в правые части уравнений.
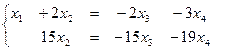
Из второго уравнения находим 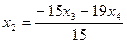 подставляя это выражение в первое уравнение, получим:
подставляя это выражение в первое уравнение, получим: 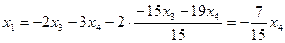
Общее решение системы:
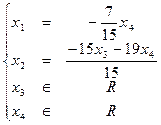
Для нахождения частных решений, свободным переменным даем произвольные значения: 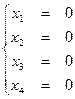
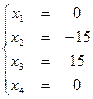
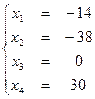
 2015-02-18
2015-02-18 343
343








