Рассмотрим систему m линейных алгебраических уравнений (СЛАУ) относительно n неизвестных 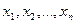 : : 
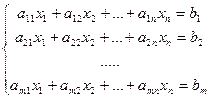 В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
В соответствии с правилом умножения матриц, рассмотренная система линейных уравнений может быть записана в матричной форме AХ=В, где
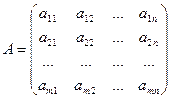 , ,
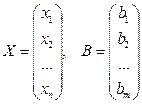 .
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения: .
Матрица A, столбцами которой являются коэффициенты при соответствующих неизвестных, а строками - коэффициенты при неизвестных в соответствующем уравнении называется матрицей системы. Матрица-столбец B, элементами которой являются правые части уравнений системы, называется столбцом свободных переменных, или просто правой частью системы. Матрица-столбец X, элементами которой являются искомые неизвестные, называется столбцом переменных.
Система линейных алгебраических уравнений, записанная в виде AX=B, является матричным уравнением.
Пример 1: Записать систему в виде матричного уравнения: 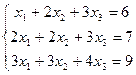 Решение: Матрица системы:
Решение: Матрица системы: 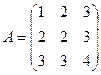 ,
столбец переменных: X= ,
столбец переменных: X= 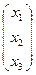 ,
столбец свободных переменных: b= ,
столбец свободных переменных: b= 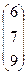 Ответ: Матричное уравнение имеет вид:
Ответ: Матричное уравнение имеет вид:
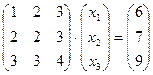 Решением системы называется совокупность n значений неизвестных
Решением системы называется совокупность n значений неизвестных
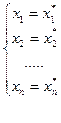 ,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца ,
при подстановке которых в систему, все уравнения обращаются в верные тождества. Или решение можно записать в виде столбца 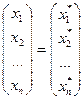 , подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА , подстановка которого в матричное уравнение AX=B, обращает его в верное тождество.
Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.
Если система имеет единственное решение, то система называется определенной, если решений много, то система называется неопределенной.
Решение матричных уравнений
Рассмотрим системы, число уравнений которых m равно числу переменных n и матрица системы А является невырожденной, т.е. detА 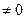 .Если матрица системы невырождена, то у нее существует обратная матрица А .Если матрица системы невырождена, то у нее существует обратная матрица А 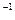 . И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А . И тогда для решения матричного уравнения AX=B, необходимо обе части этого уравнения слева умножить на А 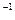 Получаем решение системы в виде: Получаем решение системы в виде: 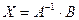 .
Пример 2: Решить систему, как матричное уравнение: .
Пример 2: Решить систему, как матричное уравнение: 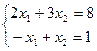 .
Решение:
1. Запишем систему в матричном виде: .
Решение:
1. Запишем систему в матричном виде: 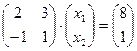 .
2. Для матрицы системы .
2. Для матрицы системы  найдем обратную матрицу: найдем обратную матрицу: 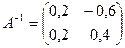 ,
3. Решение системы ищем в виде: ,
3. Решение системы ищем в виде: 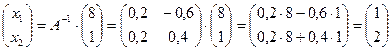 .
Ответ: .
Ответ: 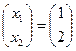 .
Пример 3: Решить матричное уравнение: .
Пример 3: Решить матричное уравнение:
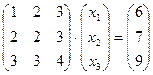 .
Решение: Для матрицы системы А найдем обратную матрицу: .
Решение: Для матрицы системы А найдем обратную матрицу:
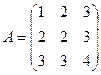 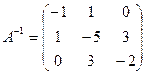 1. Решение системы ищем в виде:
1. Решение системы ищем в виде: 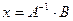 . . 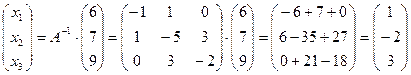 .
Ответ: .
Ответ: 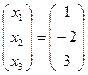 .
Правило Крамера
Справедливо следующее утверждение (формулы Крамера): .
Правило Крамера
Справедливо следующее утверждение (формулы Крамера):
Если определитель 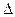 =det A матрицы системы Ax=В отличен от нуля, то система имеет единственное решение =det A матрицы системы Ax=В отличен от нуля, то система имеет единственное решение 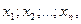 определяемое формулами Крамера: определяемое формулами Крамера: 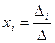 , где i=1,2,., n, , где i=1,2,., n,
| где 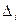 - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b. - определитель матрицы n -го порядка, полученной из матрицы A системы заменой i -го столбца столбцом свободных переменных b.
Применим правило Крамера для решения системы двух линейных уравнений с двумя неизвестными.
Рассмотрим систему: 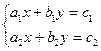 , ,
где
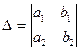 - главный определитель; - главный определитель;
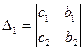 , , 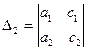 - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов. - вспомогательные определители. Они получаются заменой в главном определителе колонки коэффициентов при х (D1) и при y (D2) колонкой свободных членов.
Решение системы по правилу Крамера имеет вид:
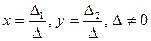 . .
Для систем трех уравнений с тремя неизвестными
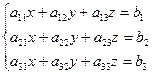
правило Крамера имеет вид:
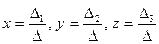 , ,
где 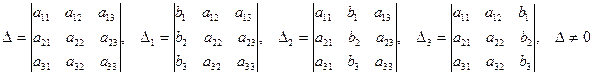
Пример 4. Решить систему по формулам Крамера: 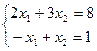 . .
Решение: 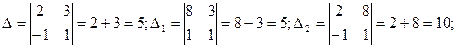
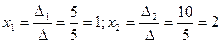
Ответ: 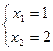
Пример 5: Решить систему по формулам Крамера: 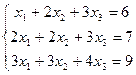
Решение: 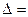 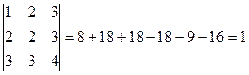
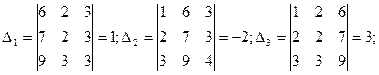
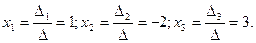
Ответ: 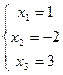
|

