2.1. Свойства Z-преобразования
Прямым Z-преобразованием дискретной последовательности xn, где n=0,1,.., называется функция комплексной переменной z, определяемая следующим соотношением
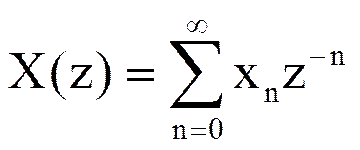 .
.
Функция определена для тех значений z, при которых ряд сходится.
Здесь и в дальнейшем последовательность обозначается строчной, а ее Z-преобразование той же прописной буквой.
Пример №1:
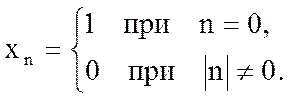
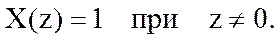
Пример №2
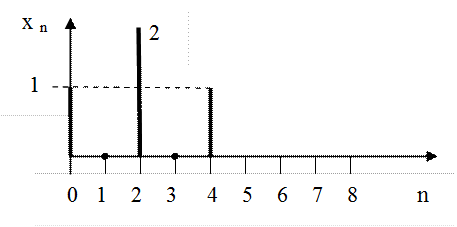
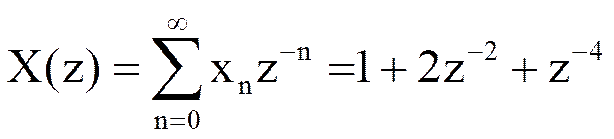
Пример №3
Найдите Z-преобразование сигнала
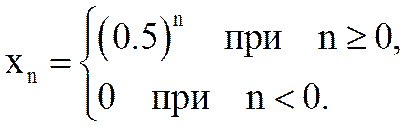
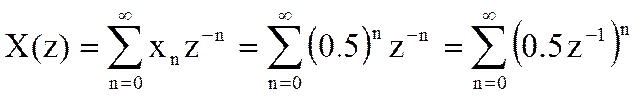 При выполнении условия
При выполнении условия 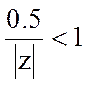
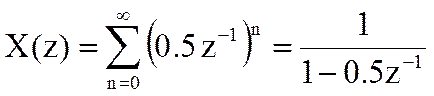
Ряд сходится в той части плоскости комплексной переменной z, для которой справедливо неравенство
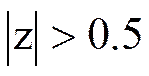
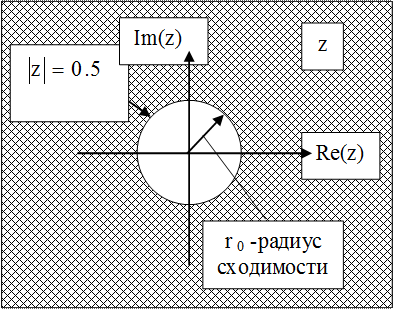
Обратное Z – преобразование
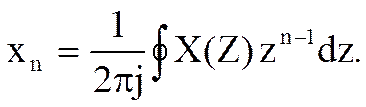
Cвойства прямого Z-преобразования.
1.Линейность. Пусть последовательность yn представляет взвешенную сумму двух последовательностей x1n и x2n
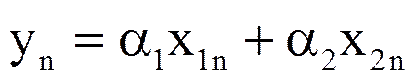 ,
,
где 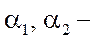 постоянные весовые коэффициенты.
постоянные весовые коэффициенты.
Тогда Z-преобразование последовательности yn определяется следующим соотношением
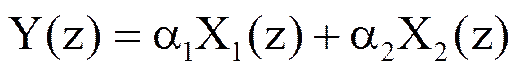 .
.
Таким образом, Z-преобразование взвешенной суммы двух последовательностей равно взвешенной сумме Z-преобразований этих последовательностей.
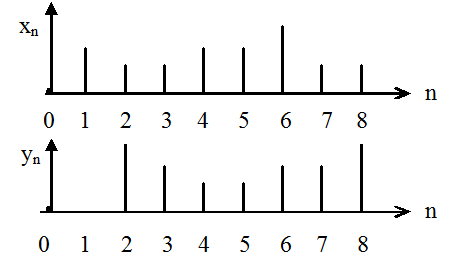
2.Сдвиг последовательностей.
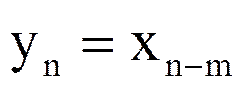
.
Последовательность yn представляет собой сдвинутую (задержанную) на m отсчетов последовательность xn
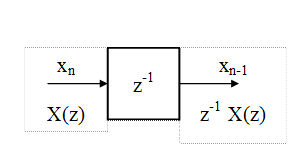
Тогда Z-преобразование Y(z) последовательности yn выражается через Z-преобразование X(z) последовательности xn следующим образом
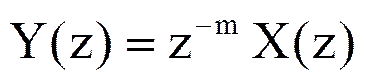 .
.
Таким образом, Z-преобразование последовательности, сдвинутой относительно исходной на m отсчетов, равно Z-преобразованию исходной последовательности, умноженной на z –m.
Пример №1
Выразите Z –преобразование Y(z) выходного сигнала yn цифровой линии задержки через Z – преобразование X(z) входного сигнала xn
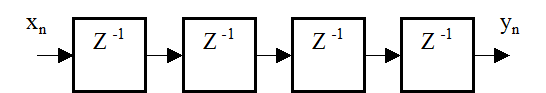
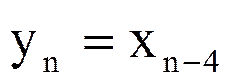
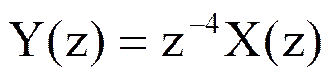
Пример №2
Выразите Z-преобразование сигнала yn через Z-преобразование сигнала xn, если
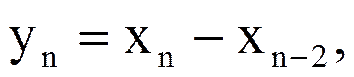
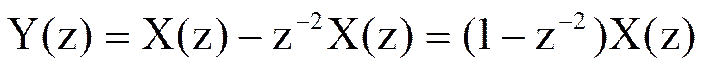
3.Дискретная свертка двух последовательностей. Дискретной сверткой двух последовательностей xn и hn называется последовательность yn,,определяемая следующим соотношением
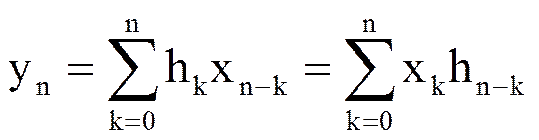
Z-преобразование Y(z) дискретной свертки двух последовательностей yn равно произведению Z-преобразований H(z) и X(z) исходных последовательностей hn и xn
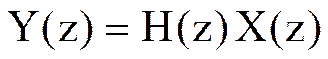 ,
,
где 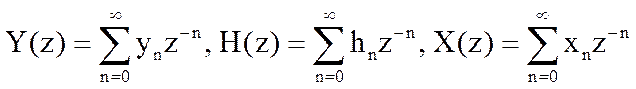 .
.
Пример
Определите Z-преобразование свертки yn дискретных сигналов
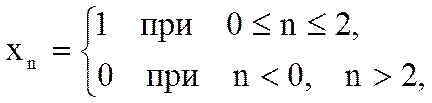
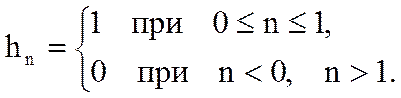
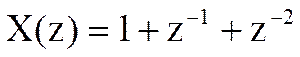
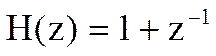
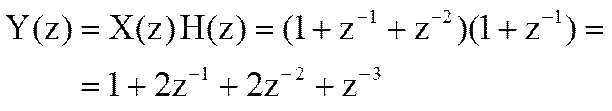
2.2. Импульсная характеристика цифрового фильтра. Понятие о рекурсивных и нерекурсивных цифровых фильтрах, БИХ- и КИХ-фильтрах
 2015-02-04
2015-02-04 944
944







