Рассмотрим степенной ряд 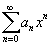 , имеющий радиус сходимости R > 0:
, имеющий радиус сходимости R > 0:
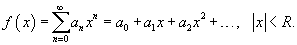
Функция 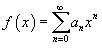 является непрерывной функцией при | x | < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой
является непрерывной функцией при | x | < R. Степенной ряд внутри интервала сходимости можно дифференцировать почленно. При этом производная степенного ряда выражается формулой
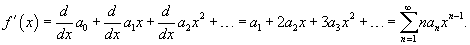
Степенной ряд можно также почленно интегрировать на отрезке, который расположен внутри интервала сходимости. Следовательно, если − R < b < x < R, то выполняется равенство
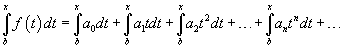
Если ряд интегрируется на отрезке [0; x ], то справедлива формула:
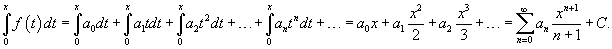
 2015-02-04
2015-02-04 2070
2070








