Система (множество, совокупность) функций, определенных на отрезке 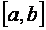 , называется ортогональной на этом отрезке, если
, называется ортогональной на этом отрезке, если 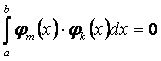 при
при 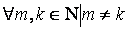 и
и
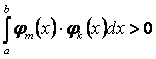 при
при 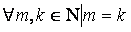 , то есть
, то есть 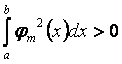 .
.
Тригонометрическим рядом Фурье функции 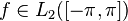 называют функциональный ряд вида
называют функциональный ряд вида
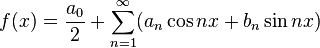
| (1) |
где
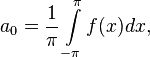
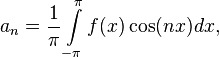
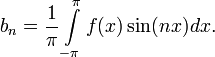
Числа 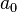 ,
, 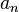 и
и 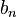 (
(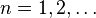 ) называются коэффициентами Фурье функции
) называются коэффициентами Фурье функции 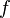 .
.
Ряд Фурье для чётной функции имеет вид:

Пусть функция 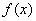 нечётная и удовлетворяет теореме Дирихле. Тогда функции
нечётная и удовлетворяет теореме Дирихле. Тогда функции 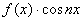 –нечётные, а
–нечётные, а
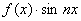 –четные при любых n =1,2,... Поэтому
–четные при любых n =1,2,... Поэтому
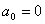 ,
, 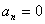 ,
, 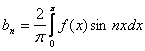 .
.
Ряд Фурье для нечётной функции имеет вид:
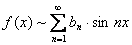 .
.
 2015-02-04
2015-02-04 676
676








