Вопрос о выборе средней решается в каждом отдельном случае, исходя из задачи исследования, материального содержания изучаемого явления или наличия исходной информации. Основное условие – величины, представляющие собой числитель и знаменатель средней, должны быть логически связаны между собой.
Средняя арифметическая – применяется в тех случаях, когда объем варьирующего признака по всей совокупности является суммой значений признаков отдельных ее частиц.
В этом случае, чтобы вычислить среднюю арифметическую, нужно сумму всех значений признаков разделить на их число.
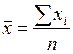
где xi – i-й вариант осредняемого признака (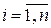 ); n – число вариант.
); n – число вариант.
Средняя, рассчитанная из вариантов, которые повторяются различное число раз, или, как говорят, имеют различный вес в совокупности, называется взвешенной:
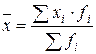 где fi – частота повторяемости i-го варианта
где fi – частота повторяемости i-го варианта
Таблица: Подвиды средней арифметической
| k | Наименование средней | Формула средней | Когда используется |
| 11 | Средняя прогрессивная или средняя передовая | Этапы ее расчета: - на основании всех данных определить среднюю, - выбрать те индивидуальные значения признака, которые лучше исчисленной средней; - из отобранных значений вычислим среднюю, которая и будет являться средней прогрессивной | |
| 22 | Средняя хронологическая простая | 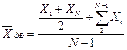 | Используется, когда размер изучаемого явления задан на определенные даты (на определенные моменты времени) |
| 33 | Средняя хронологическая взвешенная | 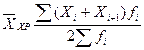 | Используется в случае, когда веса равны |
| 44 | Средняя гармоническая простая | 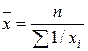 | Используется когда статистическая информация не содержит частот отдельных вариантов |
| -5 | Средняя гармоническая взвешенная | 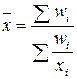 где где 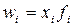 . . | Используется, когда известны ндивидуальные значения признака и веса W за ряд временных интервалов |
| 56 | Средняя геометрическая невзвешенная | 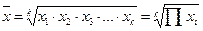 | Используется в анализе динамики для определения среднего темпа роста |
| 67 | Средняя геометрическая взвешенная | 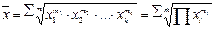 | |
| 78 | Средняя квадратическая невзвешенная | 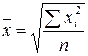 | Используется при расчете показателей вариации |
| 89 | Средняя квадратическая взвешенная | 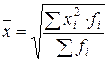 |
 2015-03-20
2015-03-20 843
843








