Выборочная средняя

х̅_в= ∑x_i

х̅_в= ∑x_in_i

выборочная средняя – среднее взвешенное знач признака с весами = соотв частотам.\

Оценка генеральной средней х_г по выборочной средней х_в

Из генеральной совокупности извлечена повторная выборка объема n: 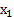… 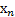– знач признака - различны.

х_г – неизв. Требуется оценить ее по данным выборки.

В качестве оценки х_г принимается х_в =

1) убедимся, что х_в – несмещенная оценка, те есть M[х_в] = х_г

Хв – СВ; 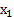… 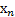– независ слу распределения СВ Х₁….Х_n, т.к. эти величины одинаково распределены à у них одинаковое мат ожидание, например М(Х)=α

М(Х_в)=М(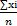) = α

Величины х₁…х_n имеют то же распределение, что и генеральная совокупность => у них одинаковые мат ожидания.

М(Х)= Х_г = α => М(Хв)= Х_г => Х_в – несмещенная оценка Х_г (Чтд)

2) Хв- состоятельная оценка Х_г

Т.к. СВ 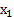… 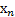имеют огранич дисперсии, то по теореме Чебышева (при ↑n => среднее арифметическое р-мых величин (то есть Хв) стремится по вероятности в мат ожиданию (=α) каждой из величин (или к Х_г, т.к. Х_г=α)).

=> при ↑n Х_в àстремиться по вероятностиà Х_г

3) если СВ Х подчиняется НЗР, то => эффективная оценка

Если генеральная средняя неизвестна и требуется оценить ее по данным выборки, то в качестве оценки генеральной средней принимают выборочную среднюю, которая является несмещенной и состоятельной оценкой. Отсюда следует, что если по нескольким выборкам достаточно большого объема из одной и той же генеральной совокупности будут найдены выборочные средние, то они будут приближенно равны между собой.

Несмещенной называют статистическую оценку 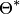, математическое ожидание которой равно оцениваемому параметру 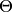, то есть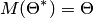

Состоятельной называют статистическую оценку, которая при 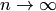стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при 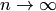стремится к нулю, то такая оценка оказывается также состоятельной.

4. Генеральная и выборочные дисперсии. Оценка генеральной дисперсии по выборочной.Асимптотические свойства оценок.

Генеральная дисперсия – среднее арифметическое кв-тов отклонений знач признака генеральн совокупности от их среднего знач Х_г.

Если 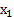… 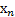- знач признака различны, D_г = ∑(x_i-x̅_г)²

Если 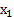… 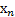имеют соотв частоты N₁….N_k, D_г = ∑(x_i-x̅_г)²*N_i

Т.е. Генеральная дисперсия – среднее взвешенное квадратов отклонений с весами = соотв частотам.

Выборочная дисперсия – среднее арифметическое кв-тов отклонений знач признака генеральн совокупности от их среднего знач Х_в.

Если 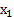… 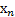- знач признака различны, D_в = ∑(x_i-x̅_в)²

Если 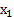… 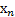имеют соотв частоты n₁….n_k, D_в = ∑(x_i-x̅_в)²*n_i

Т.е. Выборочная дисперсия – среднее взвешенное квадратов отклонений с весами = соотв частотам.

Оценка D_г по D_в

Смещенной оценкой D_г служит D_в

D_в = ∑n_i(x_i-x̅_в)² - это оценка смещенная, т.к. М(D_в)≠D_г. М(D_в) = D_г *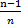

Несмещенная оценка D_г служит S² (исправленная выборочная дисперсия).

S² = 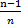* D_в = (∑n_i(x_i-x̅_в)²)*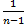

S² используется при n<30

Она несмещенная т.к. М(S²) = D_г

Оценки максимального правдоподобия могут быть асимптотически эффективными и асимптотически нормальными оценками. Асимптотическая нормальность означает, что 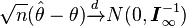где 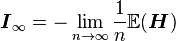асимптотическая информационная матрица. Асимптотическая эффективность означает, что асимптотическая ковариационная матрица 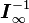является нижней границей для всех состоятельных асимптотически нормальных оценок.