Полная энергия  - электронной системы. В методе Хюккеля
- электронной системы. В методе Хюккеля 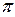 - электронная энергия молекулы равна сумме орбитальных энергий, умноженных на соответствующие числа заполнения электронами молекулярных орбиталей:
- электронная энергия молекулы равна сумме орбитальных энергий, умноженных на соответствующие числа заполнения электронами молекулярных орбиталей:
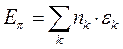
учитывая, что:
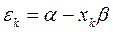
будем иметь соответственно:
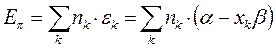
Используя полученное выражение, вычислим  - электронные энергии молекул линейных полиенов (чётных и нечётных), рассмотренных нами уже выше.
- электронные энергии молекул линейных полиенов (чётных и нечётных), рассмотренных нами уже выше.
Поскольку:
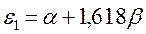
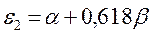
тогда после подстановки данных выражений в уравнение вида:
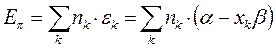
а также учитывая, что 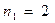 и
и 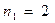 - полностью заполненные молекулярные орбитали, будем иметь соответственно:
- полностью заполненные молекулярные орбитали, будем иметь соответственно:
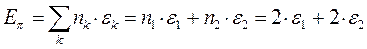
здесь:
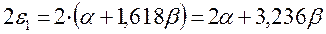
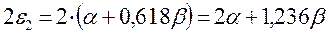
подставляя полученные выражения в уравнение:
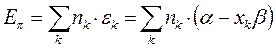
будем иметь соответственно:
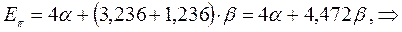
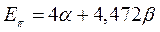
Энергия делокализации. Энергия делокализации является фундаментальной характеристикой устойчивости сопряжённой системы. Она характеризует тот выигрыш в энергии, который имеет место при существующей в молекуле делокализации  - электронов. Энергия делокализации определяется как разность между общей энергией
- электронов. Энергия делокализации определяется как разность между общей энергией  - электронной системы молекулы и энергией системы с локализованными (фиксированными) связями:
- электронной системы молекулы и энергией системы с локализованными (фиксированными) связями:
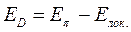
здесь 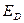 - энергия делокализации
- энергия делокализации  - электронной системы,
- электронной системы, 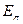 - полная энергия
- полная энергия  - электронной системы и
- электронной системы и 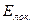 - энергия системы с локализованными связями.
- энергия системы с локализованными связями.
Принимая при этом, что:
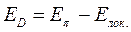
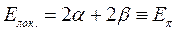
будем иметь соответственно:
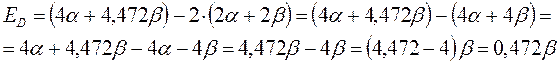
Энергия диссоциации  - связи. Энергия связи является фундаментальной характеристикой молекулярной системы, характеризуя ту энергию, которая необходима для её разрыва (энергия диссоциации). Энергия связи коррелирует с порядком связи. По её значению можно делать выводы относительно прочности химической связи и её длины. Данный параметр можно вычислить исходя из следующих соображений:
- связи. Энергия связи является фундаментальной характеристикой молекулярной системы, характеризуя ту энергию, которая необходима для её разрыва (энергия диссоциации). Энергия связи коррелирует с порядком связи. По её значению можно делать выводы относительно прочности химической связи и её длины. Данный параметр можно вычислить исходя из следующих соображений:
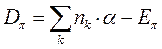
учитывая, что:
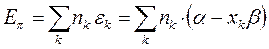
будем иметь соответственно:
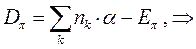
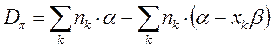
используя выведенное выше уравнение:
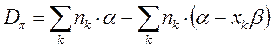
рассчитаем энергии диссоциации  - связи в молекулах линейных полиенов.
- связи в молекулах линейных полиенов.
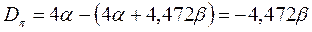
Энергии ВЗМО и НСМО. Значения этих величин получают путём решения векового детерминанта. Они отвечают соответственно энергиям ионизации (ВЗМО) и сродства к электрону (НСВМ). Как известно в методе Хюккеля (МОХ) оперируют с параметрами 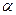 и
и 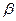 , значения которых значения берётся из эксперимента. Так, значение кулоновского интеграла
, значения которых значения берётся из эксперимента. Так, значение кулоновского интеграла 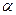 на основании теоремы Купманса можно оценить по значению энергии ионизации
на основании теоремы Купманса можно оценить по значению энергии ионизации 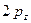 -орбитали и в случае атома водорода
-орбитали и в случае атома водорода 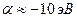 . Резонансный интеграл
. Резонансный интеграл 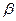 определяет выигрыш в энергии при образовании химической связи. Кулоновские интегралы одинаковы для всех атомов углерода, а резонансные (обменные) интегралы одинаковы для всех углерод – углеродных связей, принимая значение
определяет выигрыш в энергии при образовании химической связи. Кулоновские интегралы одинаковы для всех атомов углерода, а резонансные (обменные) интегралы одинаковы для всех углерод – углеродных связей, принимая значение 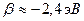 . Используя значения этих интегралов, рассчитаем энергии ионизации и сродства к электрону рассматриваемых сопряжённых молекул. Согласно теореме Купманса, потенциал ионизации есть орбитальная энергия, взятая с обратным знаком. Аналогичная связь имеется также между знаком орбитальной энергии низшей свободной молекулярной орбитали и сродством к электрону, т.е. имеем соответственно:
. Используя значения этих интегралов, рассчитаем энергии ионизации и сродства к электрону рассматриваемых сопряжённых молекул. Согласно теореме Купманса, потенциал ионизации есть орбитальная энергия, взятая с обратным знаком. Аналогичная связь имеется также между знаком орбитальной энергии низшей свободной молекулярной орбитали и сродством к электрону, т.е. имеем соответственно:
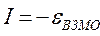
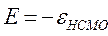
Таким образом, имеем соответственно:
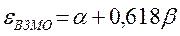
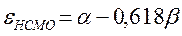
поскольку:
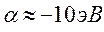
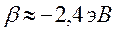
тогда соответственно:
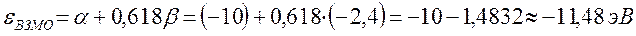
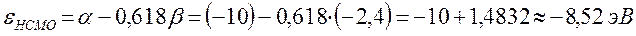
учитывая, что:
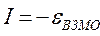
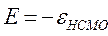
имеем соответственно:
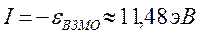
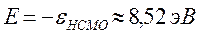
 2015-03-22
2015-03-22 672
672








