Электронная плотность. В методе Хюккеля электронная плотность на атоме 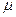 вычисляется на основании формулы вида:
вычисляется на основании формулы вида:
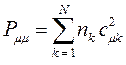
здесь 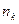 - число электронов на молекулярной орбитали
- число электронов на молекулярной орбитали 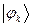 с номером
с номером 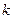 .
.
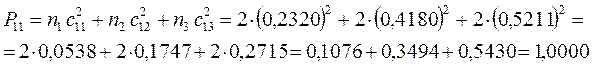
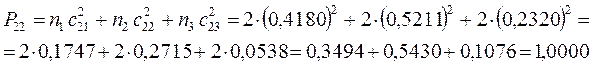
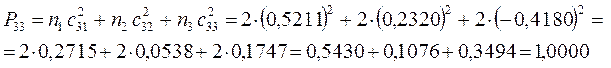
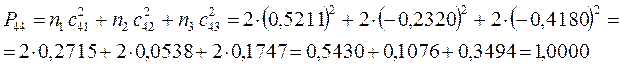
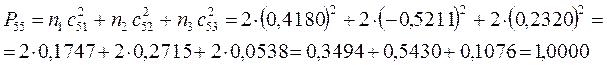
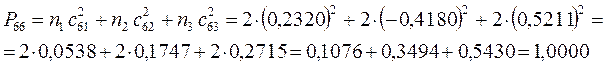
поскольку:
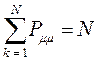
имеем таким образом:
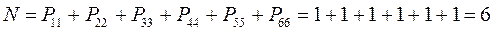
Заряд на атоме. Поскольку в результате делокализации некоторая часть  - электронов сосредотачивается у атома
- электронов сосредотачивается у атома 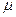 , то в силу этого, электронная плотность на этом атоме
, то в силу этого, электронная плотность на этом атоме 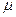 будет равна
будет равна 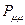 . Очевидно, разность величин
. Очевидно, разность величин 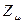 и
и 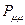 будет определять остаточный заряд, который будет сосредотачиваться у данного атома:
будет определять остаточный заряд, который будет сосредотачиваться у данного атома:
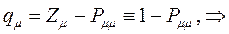
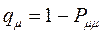
Поскольку, как было показано выше:
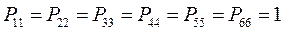
тогда соответственно:
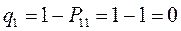
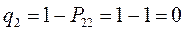
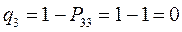
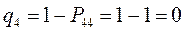
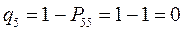
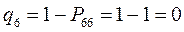
т.е. имеем:
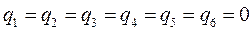
Порядок связи. Поскольку в приближении ЛКАО – МО,  - электроны делокализованны по всей молекуле, то вклад в образование
- электроны делокализованны по всей молекуле, то вклад в образование  - связи между любой парой атомов будут вносить электроны всех заполненных молекулярных орбиталей. В методе Хюккеля порядок связи вычисляют по формуле вида:
- связи между любой парой атомов будут вносить электроны всех заполненных молекулярных орбиталей. В методе Хюккеля порядок связи вычисляют по формуле вида:
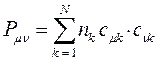
По аналогии с трактовкой 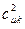 произведение орбитальных коэффициентов
произведение орбитальных коэффициентов 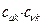 можно интерпретировать как плотность электронов, сосредоточенную между двумя атомами
можно интерпретировать как плотность электронов, сосредоточенную между двумя атомами 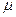 и
и 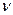 . В общем случае, в приближении Хюккеля, порядок связи будет характеризовать степень
. В общем случае, в приближении Хюккеля, порядок связи будет характеризовать степень  - электронного связывания. Воспользовавшись коэффициентами входящих в выражения для связывающих молекулярных орбиталей
- электронного связывания. Воспользовавшись коэффициентами входящих в выражения для связывающих молекулярных орбиталей 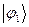 и
и 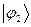 , учитывая при этом, что
, учитывая при этом, что 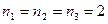 , будем иметь:
, будем иметь:
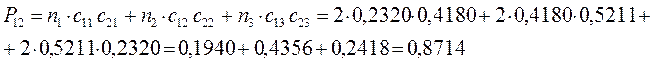
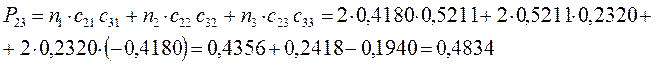
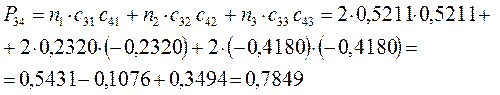
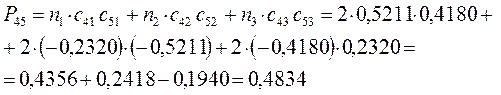
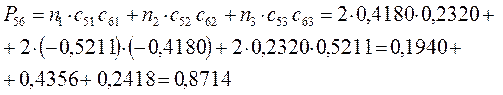
Принимая порядок локализованной 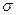 - связи равным единице
- связи равным единице 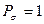 , получим полный порядок кратной
, получим полный порядок кратной 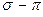 - связи, который будет равен соответственно:
- связи, который будет равен соответственно:
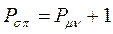
откуда следует, что:
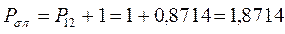
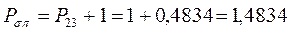
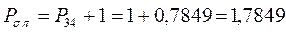
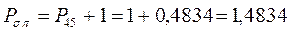
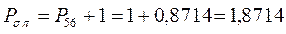
все возможные для данной системы величины 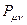 соберём в матрицу плотности первого порядка
соберём в матрицу плотности первого порядка 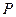 размером
размером 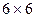 :
:
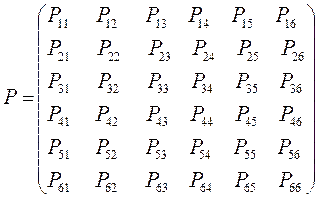
здесь диагональные элементы представляют собой электронные плотности на атомах 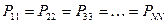 , а недиагональные – порядки связей. Как уже было установлено ранее:
, а недиагональные – порядки связей. Как уже было установлено ранее:
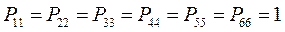
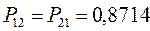
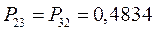
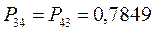
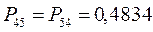
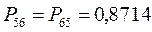
Для построения матрицы плотности первого порядка, рассчитаем также дальние порядки связей, которые для некоторых классов органических реакций могут быть использованы как индексы реакционной способности:
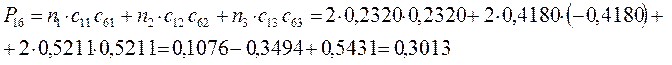 поскольку матрица порядков связей симметрична
поскольку матрица порядков связей симметрична 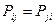 , тогда соответственно:
, тогда соответственно:
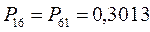
Учитывая приведенные выше данные, строим матрицу порядков связи в виде:
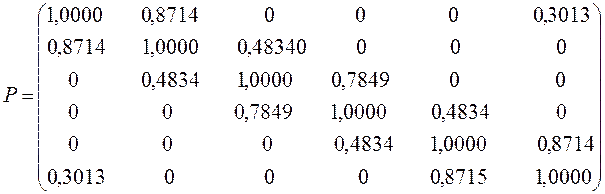
Индекс свободной валентности. Поскольку полный порядок связи 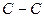 может иметь различные значения, то соответственно этому и реакционная способность атомов углерода может быть также различной. Мерой реакционной способности молекулы является индекс свободной валентности, который определяют как разность между максимально возможным полным порядком связей и реальным полным порядком связей данного атома. Индекс свободной валентности на атоме
может иметь различные значения, то соответственно этому и реакционная способность атомов углерода может быть также различной. Мерой реакционной способности молекулы является индекс свободной валентности, который определяют как разность между максимально возможным полным порядком связей и реальным полным порядком связей данного атома. Индекс свободной валентности на атоме 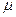 вычисляют по формуле:
вычисляют по формуле:
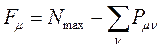
где 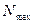 - максимально возможная сумма порядков связей атома углерода в сопряжённой системе, а
- максимально возможная сумма порядков связей атома углерода в сопряжённой системе, а 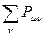 - сумма порядков связей данного атома
- сумма порядков связей данного атома 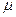 со всеми соседними атомами. Поскольку, как показывают расчёты:
со всеми соседними атомами. Поскольку, как показывают расчёты:
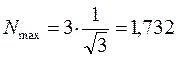
в связи с этим при вычислениях удобно использовать формулу вида:
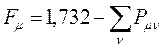
учитывая, что:
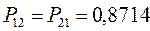
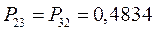
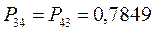
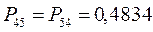
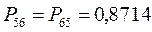
после подстановки будем иметь соответственно:
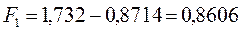
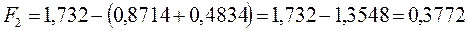
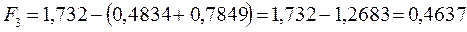
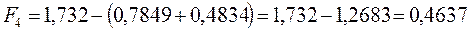
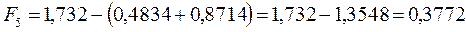
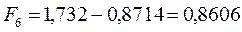
6.1.4. Октатетраен: 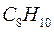
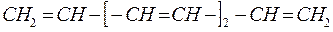
Изобразим граф рассматриваемой молекулы октатетраена и пронумеруем атомы углерода, входящие в её состав:

Рис. 14. Граф молекулы октатетраена.
На основании данных о молекулярном графе и виде топологической матрицы (или матрицы смежности), передающих информацию о молекулярной структуре сопряжённых и ароматических соединений, с учётом введенного орбитального параметра 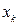 , составим хюккелевский детерминант, порядок которого очевидно будет равен общему числу атомов углерода в молекуле:
, составим хюккелевский детерминант, порядок которого очевидно будет равен общему числу атомов углерода в молекуле:
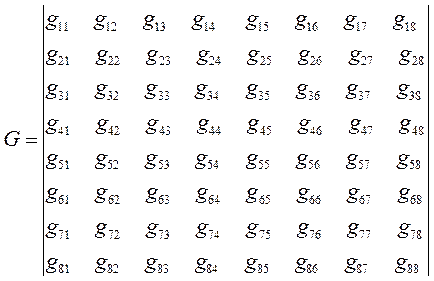
Полагая значения диагональных матричных элементов равными 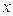 и далее, присваивая значения 1 тем недиагональным матричным элементам, которые соответствуют соседним атомам (между которыми имеет место химическая связь) и нуль тем недиагональным матричным элементам, которые отвечают несоседним атомам (между которыми химической связи нет), приходим к выражению вида:
и далее, присваивая значения 1 тем недиагональным матричным элементам, которые соответствуют соседним атомам (между которыми имеет место химическая связь) и нуль тем недиагональным матричным элементам, которые отвечают несоседним атомам (между которыми химической связи нет), приходим к выражению вида:
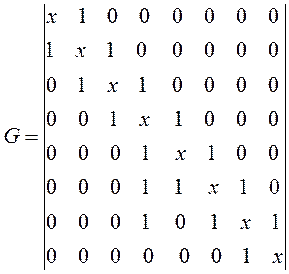
полученный таким образом детерминант приравнивают нулю, т.е. имеем:
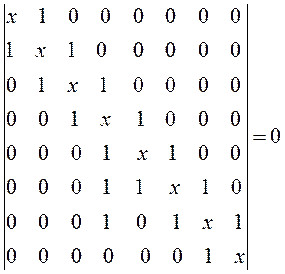
Наиболее простой путь решения детерминанта такого типа является метод, предложенный Ч. Коулсоном. Понижение порядка детерминанта такого типа, когда число атомов углерода в молекуле полиена 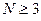 , производится на основании общей формулы вида:
, производится на основании общей формулы вида:
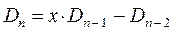
имеем:
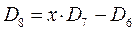
учитывая, что:
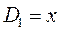
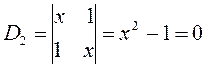
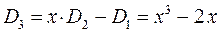
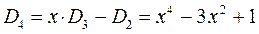
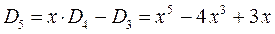
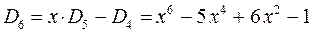
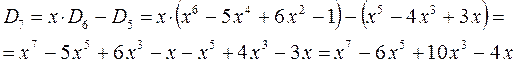
находим для октатетраена выражение вида:
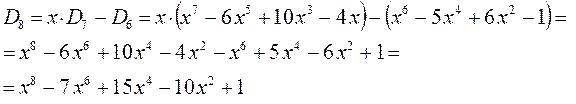
откуда следует, что:
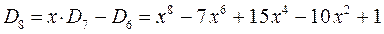
На основании общих решений векового детерминанта, рассчитаем значения орбитальных параметров, энергий и коэффициентов разложения, для случая молекулы октатетраена:
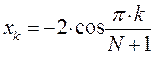
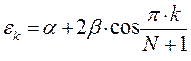
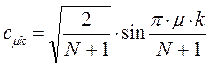
здесь 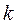 - индекс молекулярной орбитали,
- индекс молекулярной орбитали, 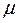 - индекс атомной орбитали и величина
- индекс атомной орбитали и величина 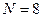 есть число атомов углерода в цепи сопряжения.
есть число атомов углерода в цепи сопряжения.
Поскольку:
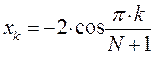
тогда после подстановки соответствующих величин, будем иметь:
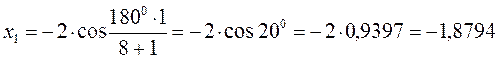
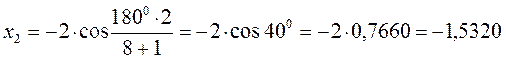
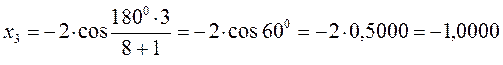
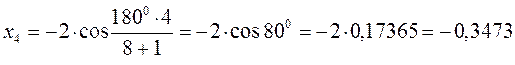
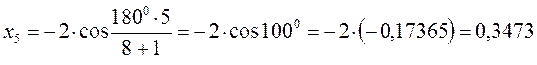
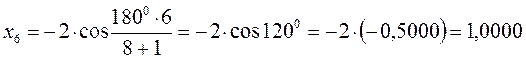
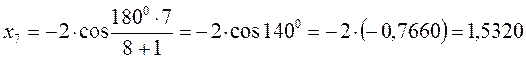
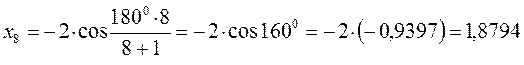
Поскольку:
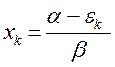
имеем:
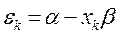
учитывая, что:
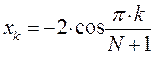
имеем:
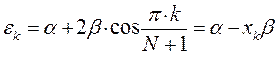
или после подстановки значений орбитальных параметров:
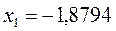
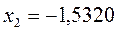
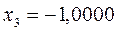
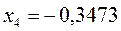
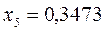
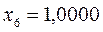
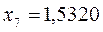
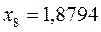
в уравнение вида:
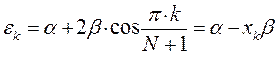
получаем набор орбитальных энергий связывающего и соответственно разрыхляющего состояний рассматриваемой системы:
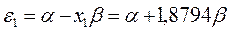
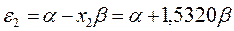
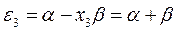
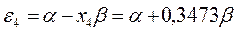
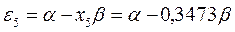
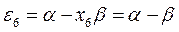
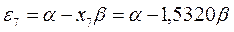
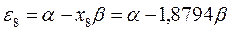
Таким образом, будем иметь соответственно:
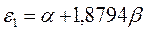
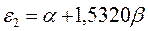
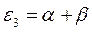
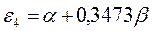
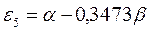
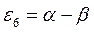
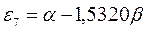
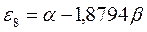
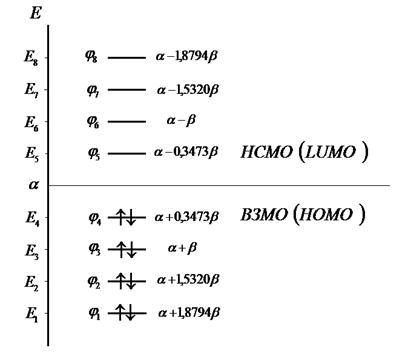
Рис. 15. Диаграмма энергетических уровней молекулы октатетраена
(основное состояние).
На основании выражения вида:
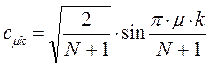
рассчитаем теперь значения орбитальных коэффициентов и построим аналитические выражения для связывающей и разрыхляющей молекулярных орбиталей октатетраена. Учитывая, разложение молекулярной орбитали 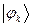 по базисному набору соответствующих атомных орбиталей
по базисному набору соответствующих атомных орбиталей 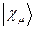 :
:
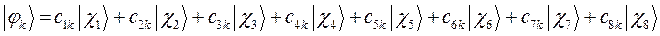
здесь: 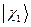 ,
, 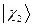 ,
, 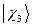 ,
, 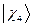 ,
, 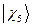 ,
, 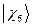 ,
, 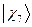 и
и 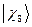 - атомные
- атомные 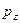 - орбитали слэйтеровского типа,
- орбитали слэйтеровского типа, 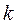 - индекс молекулярной орбитали,
- индекс молекулярной орбитали, 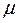 - индекс атомной орбитали и величина
- индекс атомной орбитали и величина 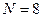 есть число атомов углерода в цепи сопряжения. Расчитаем орбитальные коэффициенты для самой низкой в энергетическом отношении молекулярной орбитали
есть число атомов углерода в цепи сопряжения. Расчитаем орбитальные коэффициенты для самой низкой в энергетическом отношении молекулярной орбитали 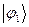 :
:
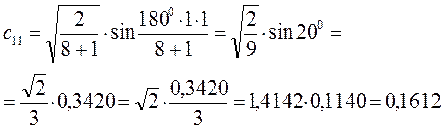
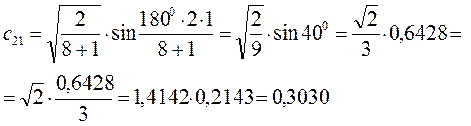
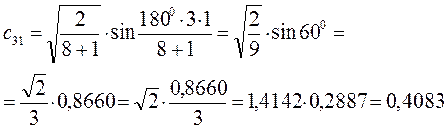
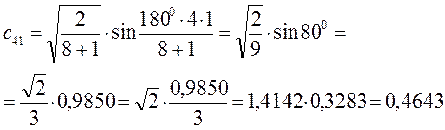
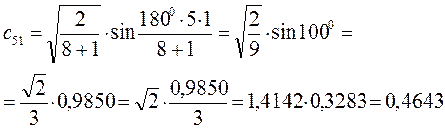
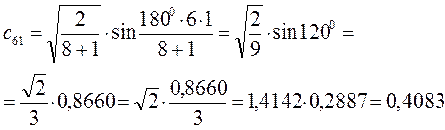
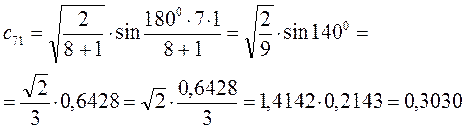
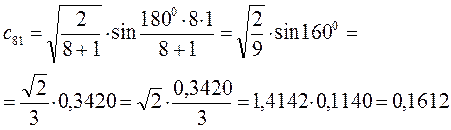
Рассчитаем теперь орбитальные коэффициенты для молекулярной орбитали 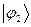 :
:
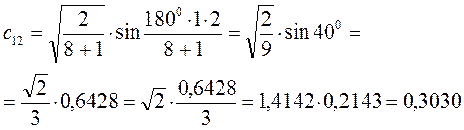
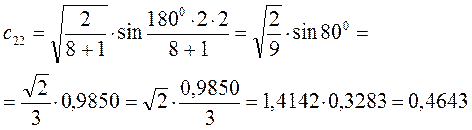
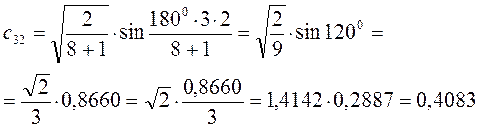
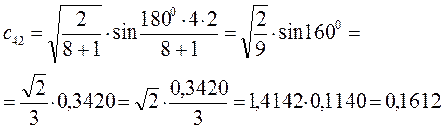
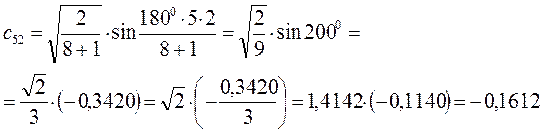
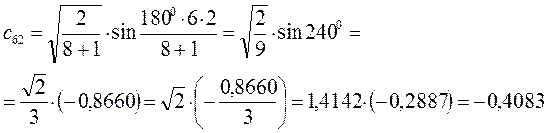
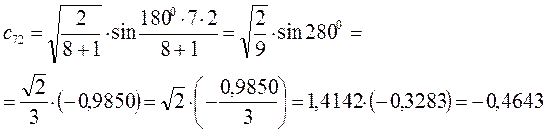
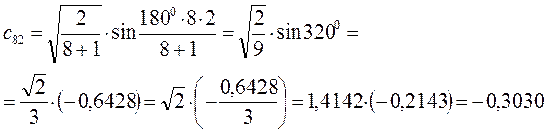
Рассчитаем теперь орбитальные коэффициенты для молекулярной орбитали 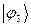 , в результате будем иметь соответственно:
, в результате будем иметь соответственно:
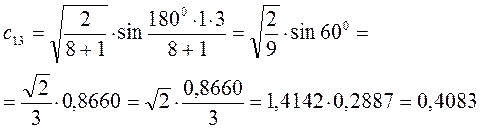
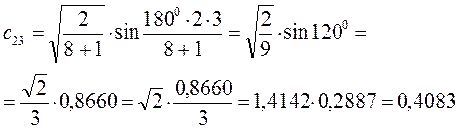
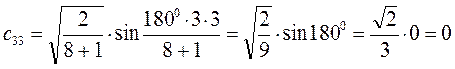
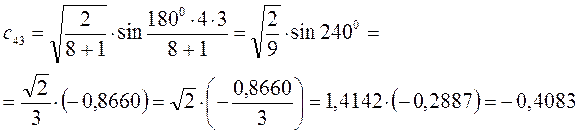
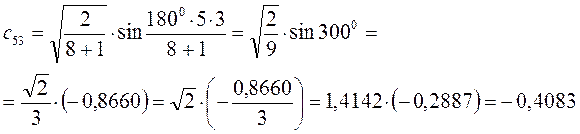
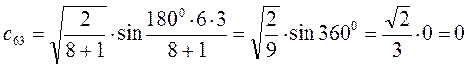
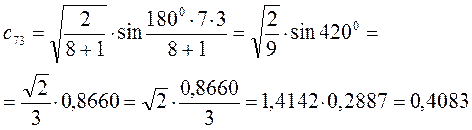
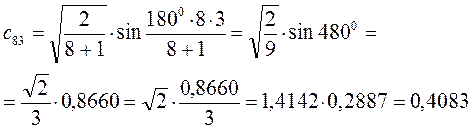
Рассчитаем орбитальные коэффициенты для молекулярной орбитали 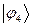 :
:
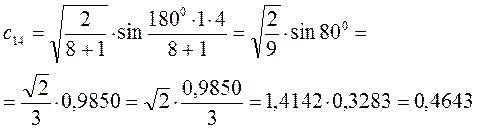
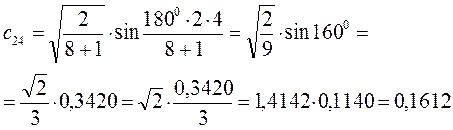
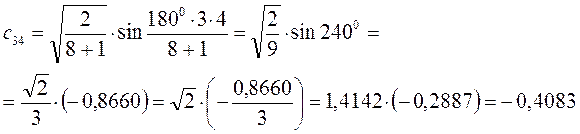
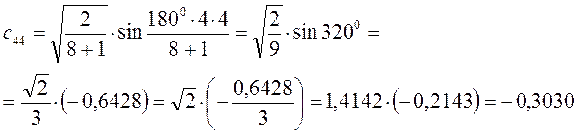
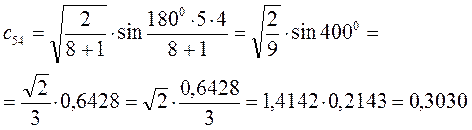
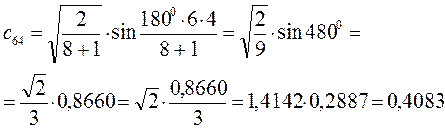
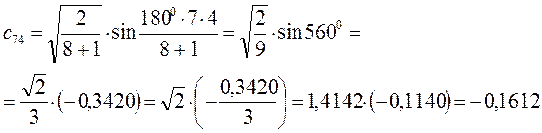
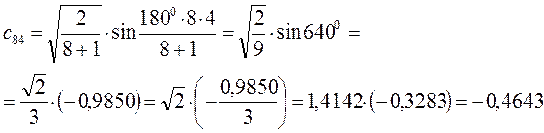
Рассчитаем орбитальные коэффициенты для молекулярной орбитали 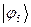 :
:
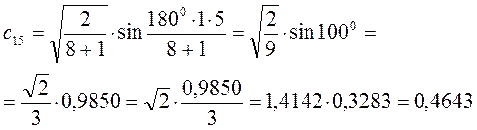
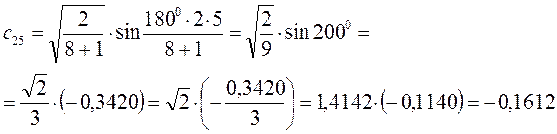
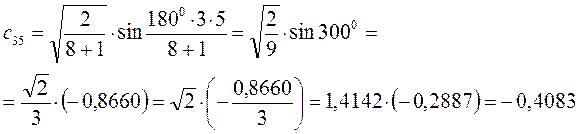
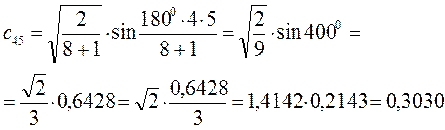
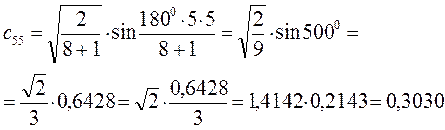
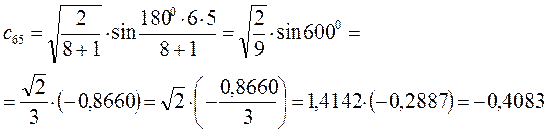
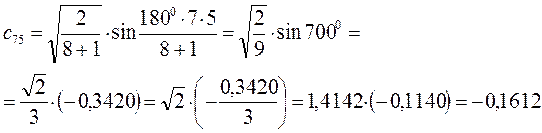
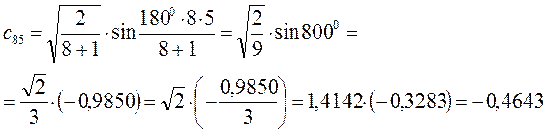
Рассчитаем орбитальные коэффициенты для молекулярной орбитали 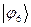 :
:
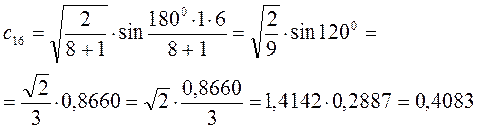
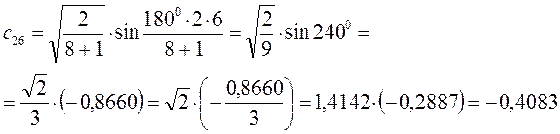
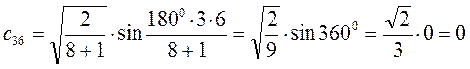
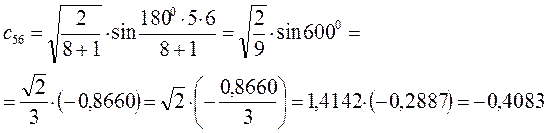
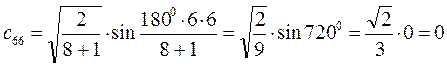
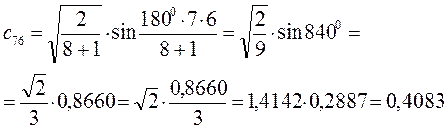
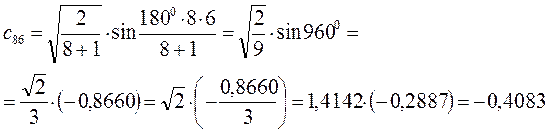
Рассчитаем орбитальные коэффициенты для молекулярной орбитали 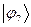 :
:
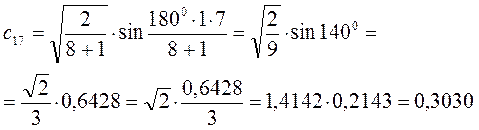
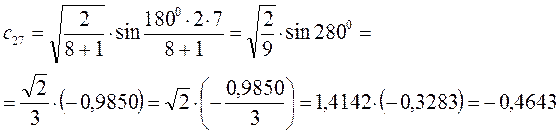
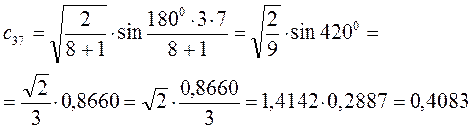
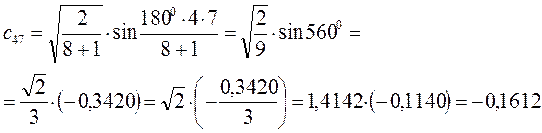
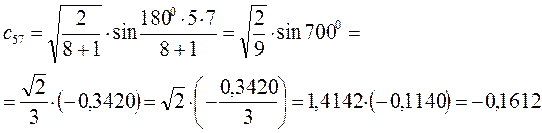
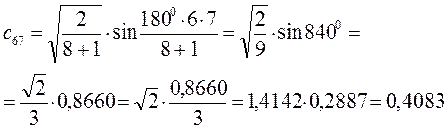
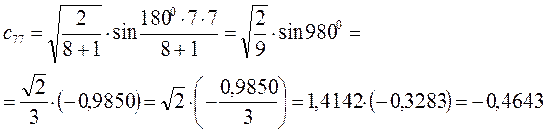
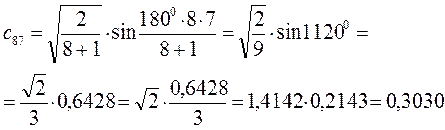
Рассчитаем орбитальные коэффициенты для молекулярной орбитали 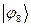 :
:
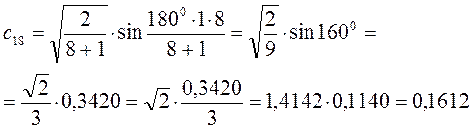
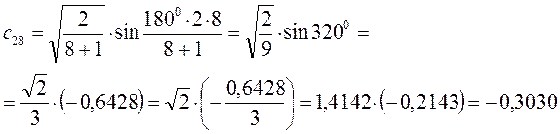
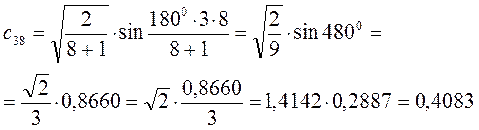
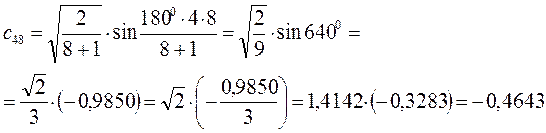
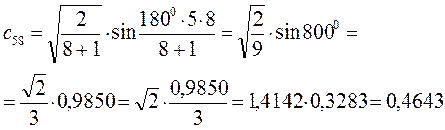
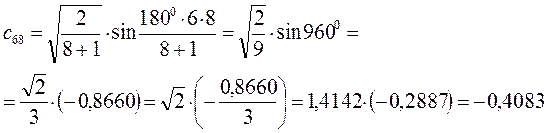
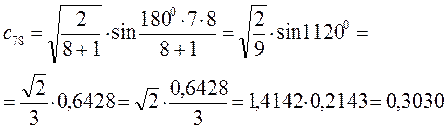
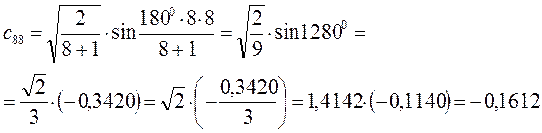
В ходе проделанных выше выкладок, приходим к выражениям для энергий и соответствующих им волновых функций связывающего и разрыхляющего состояний октатетраена, полученных в ходе решения хюккелевского детерминанта 8-го порядка 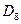 .
.
Таблица 14. Энергии связывающей и разрыхляющей молекулярных орбиталей молекулы октатетраена.
| Симметрия МО | Орбитальный параметр, 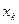 | Энергия МО, 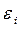 | МО, 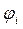 |
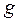 | 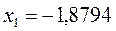 | 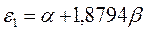 | 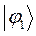 |
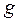 | 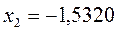 | 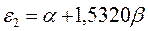 | 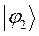 |
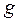 | 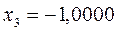 | 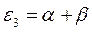 | 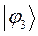 |
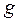 | 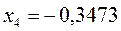 | 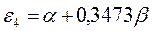 | 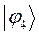 |
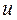 | 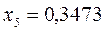 | 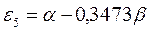 | 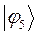 |
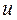 | 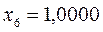 | 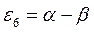 | 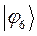 |
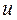 | 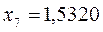 | 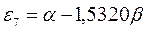 | 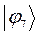 |
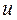 | 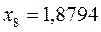 | 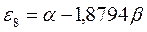 | 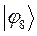 |
Таблица 15. Значения орбитальных коэффициентов.
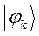 | 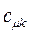 | 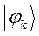 | 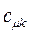 |
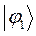 | 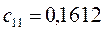 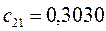 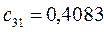 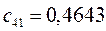 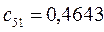 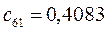 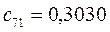 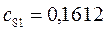 | 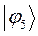 | 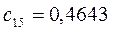 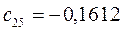 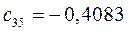 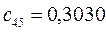 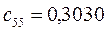 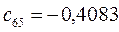 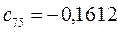 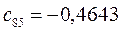 |
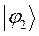 | 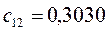 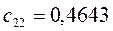 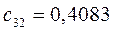 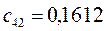 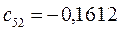 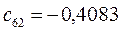 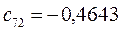 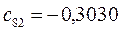 | 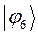 | 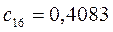 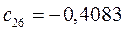 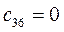 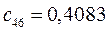 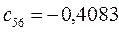 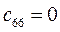 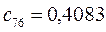 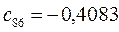 |
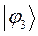 | 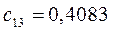 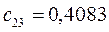 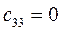 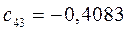 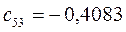 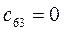 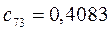 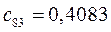 | 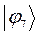 | 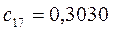 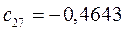 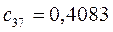 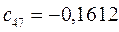 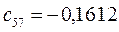 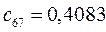 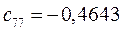 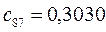 |
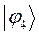 | 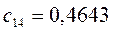 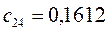 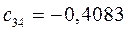 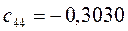 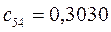 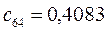 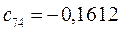 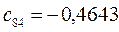 | 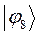 | 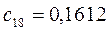 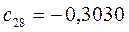 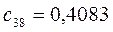 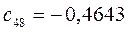 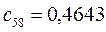 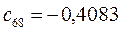 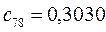 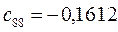 |
Учитывая разложение молекулярной орбитали 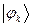 по базисному набору соответствующих атомных орбиталей
по базисному набору соответствующих атомных орбиталей 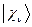 :
:
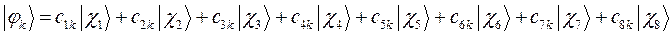
а также учитывая значения полученных выше коэффициентов разложения 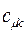 для каждой из молекулярных орбиталей, будем иметь соответственно выражения для волновых функций связывающего и разрыхляющего состояний:
для каждой из молекулярных орбиталей, будем иметь соответственно выражения для волновых функций связывающего и разрыхляющего состояний:
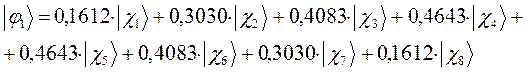
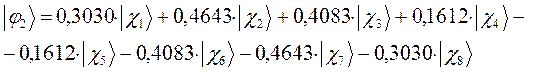
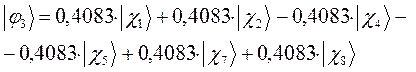
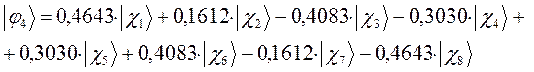
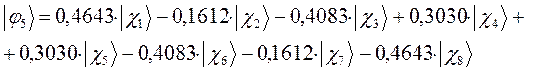
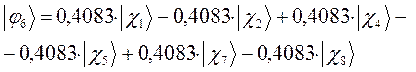
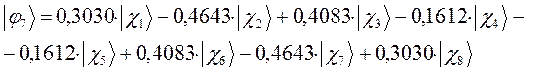
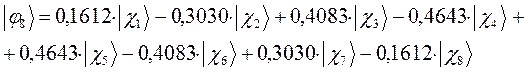
 2015-03-22
2015-03-22 1206
1206
