Электронная плотность: Из рассмотрения диаграммы энергетических уровней этилена хорошо видно, что электронная плотность на первом и втором атомах углерода создаётся за счёт двух электронов находящихся на молекулярной орбитали 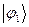 (здесь
(здесь 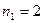 ). Учитывая значения орбитальных коэффициентов полученных для молекулярной орбитали
). Учитывая значения орбитальных коэффициентов полученных для молекулярной орбитали 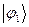 , на основании формулы вида:
, на основании формулы вида:
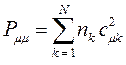
где 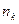 - число электронов на молекулярной орбитали
- число электронов на молекулярной орбитали 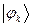 с номером
с номером 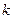 , вычислим электронные плотности на каждом
, вычислим электронные плотности на каждом 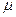 - атомах. Последние отражают ту долю заряда
- атомах. Последние отражают ту долю заряда  - электронов, которые находятся у данного атома.Поскольку по-определению:
- электронов, которые находятся у данного атома.Поскольку по-определению:
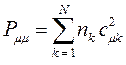
в результате будем иметь соответственно:
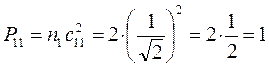
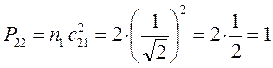
при этом сумма электронных плотностей на всех атомах, очевидно должна быть равна общему числу  - электронов системы. Подстановка соответствующих значений парциальных плотностей
- электронов системы. Подстановка соответствующих значений парциальных плотностей 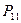 и
и 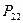 в выражение:
в выражение:
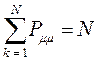
должно очевидно дать число электронов принимающих участие в образовании  - электронной системы рассматриваемой молекулы. Таким образом, будем иметь соответственно:
- электронной системы рассматриваемой молекулы. Таким образом, будем иметь соответственно:
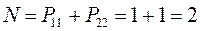
Заряд на атоме. Поскольку в результате делокализации некоторая часть  - электронов сосредотачивается у атома
- электронов сосредотачивается у атома 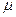 , то в силу этого, электронная плотность на этом атоме
, то в силу этого, электронная плотность на этом атоме 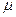 будет равна
будет равна 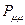 . Очевидно, разность величин
. Очевидно, разность величин 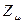 и
и 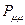 будет определять остаточный заряд, который будет сосредотачиваться у данного атома:
будет определять остаточный заряд, который будет сосредотачиваться у данного атома:
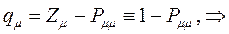
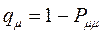
как было показано выше:
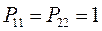
тогда соответственно:
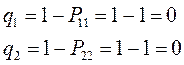
т.е. имеем:
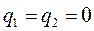
Порядок связи. Поскольку в приближении ЛКАО – МО,  - электроны делокализованны по всей молекуле, то вклад в образование
- электроны делокализованны по всей молекуле, то вклад в образование  - связи между любой парой атомов будут вносить электроны всех заполненных молекулярных орбиталей. В результате порядок связи будет отличаться от целочисленной величины.
- связи между любой парой атомов будут вносить электроны всех заполненных молекулярных орбиталей. В результате порядок связи будет отличаться от целочисленной величины.
В методе Хюккеля порядок связи вычисляют по формуле вида:
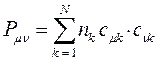
Воспользовавшись коэффициентами связывающей молекулярной орбитали 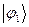 , учитывая при этом, что
, учитывая при этом, что 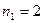 , будем иметь соответственно:
, будем иметь соответственно:
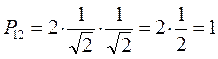
По аналогии с трактовкой 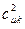 произведение орбитальных коэффициентов
произведение орбитальных коэффициентов 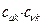 можно интерпретировать как плотность электронов, сосредоточенную между двумя атомами
можно интерпретировать как плотность электронов, сосредоточенную между двумя атомами 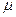 и
и 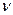 . В общем случае, в приближении Хюккеля, порядок связи будет характеризовать степень
. В общем случае, в приближении Хюккеля, порядок связи будет характеризовать степень  - электронного связывания. Порядок локализованной
- электронного связывания. Порядок локализованной 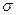 - связи принимают равным единице
- связи принимают равным единице 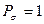 . Очевидно полный порядок кратной
. Очевидно полный порядок кратной 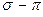 - связи будет равен:
- связи будет равен:
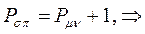
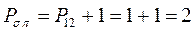
т.е. имеем соответственно:
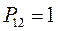
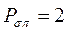
Все возможные для данной системы величины 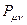 оказывается удобным собирать последние в матрицу 2-го порядка размерности
оказывается удобным собирать последние в матрицу 2-го порядка размерности 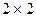 . Такую матрицу
. Такую матрицу 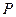 называют матрицей порядков связей (или матрицей плотности первого порядка):
называют матрицей порядков связей (или матрицей плотности первого порядка):
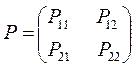
здесь диагональные элементы будут представлять собой электронные плотности на атомах 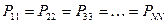 , а недиагональные – порядки связей. Как было установлено:
, а недиагональные – порядки связей. Как было установлено:
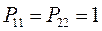
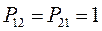
тогда соответственно:
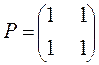
Матрица порядков связей симметрична 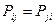 . В хюккелевских расчётах молекул сопряжённых систем порядок связи между парами химически связанных атомов является относительно большой и положительной величиной. Следовательно, делокализация
. В хюккелевских расчётах молекул сопряжённых систем порядок связи между парами химически связанных атомов является относительно большой и положительной величиной. Следовательно, делокализация  - электронов двойных связей происходит по всей молекуле. Это в свою очередь означает, что в молекулах, где имеет место сопряжение, двойная связь существует в определённой мере между всеми атомами углерода. Результаты расчёта электронных плотностей и порядков связей, наносят на молекулярную диаграмму. Порядок связи тесно связан с такими характеристиками связей в молекуле, как силовая постоянная, рефракция и межатомное расстояние. Поскольку порядок связи
- электронов двойных связей происходит по всей молекуле. Это в свою очередь означает, что в молекулах, где имеет место сопряжение, двойная связь существует в определённой мере между всеми атомами углерода. Результаты расчёта электронных плотностей и порядков связей, наносят на молекулярную диаграмму. Порядок связи тесно связан с такими характеристиками связей в молекуле, как силовая постоянная, рефракция и межатомное расстояние. Поскольку порядок связи 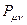 представляет собой величину, характеризующую насыщенность углерод – углеродной связи
представляет собой величину, характеризующую насыщенность углерод – углеродной связи  - электронами, то очевидно, увеличение порядок связи будет приводить к сокращению длины связи, поскольку в этом случае ядра должны как бы стягиваться к центру связи. Это в свою очередь позволяет предполагать обратную зависимость порядка связи от её длины:
- электронами, то очевидно, увеличение порядок связи будет приводить к сокращению длины связи, поскольку в этом случае ядра должны как бы стягиваться к центру связи. Это в свою очередь позволяет предполагать обратную зависимость порядка связи от её длины:
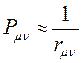
Индекс свободной валентности. Поскольку полный порядок связи 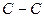 может иметь различные значения, то соответственно этому и реакционная способность атомов углерода может быть также различной. Мерой реакционной способности молекулы является индекс свободной валентности, который определяют как разность между максимально возможным полным порядком связей и реальным полным порядком связей данного атома.
может иметь различные значения, то соответственно этому и реакционная способность атомов углерода может быть также различной. Мерой реакционной способности молекулы является индекс свободной валентности, который определяют как разность между максимально возможным полным порядком связей и реальным полным порядком связей данного атома.
Индекс свободной валентности на атоме 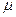 вычисляют по формуле:
вычисляют по формуле:
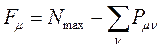
поскольку:
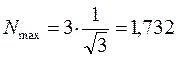
тогда:
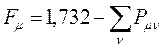
учитывая, что:
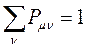
будем иметь соответственно:
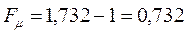
откуда следует, что:
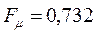
Индекс свободной валентности 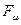 характеризует степень участия данного атома в
характеризует степень участия данного атома в  - электронной системе. Его используют для предсказания способности сопряжённой системы принимать участие в радикальных реакциях. Индекс свободной валентности
- электронной системе. Его используют для предсказания способности сопряжённой системы принимать участие в радикальных реакциях. Индекс свободной валентности 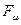 обычно изображают на молекулярной диаграмме рядом со стрелкой, которую выводят из соответствующей вершины молекулярного графа.
обычно изображают на молекулярной диаграмме рядом со стрелкой, которую выводят из соответствующей вершины молекулярного графа.
6.1.2. Бутадиен: 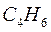
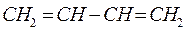
Изобразим граф рассматриваемой молекулы бутадиена и пронумеруем атомы углерода, входящие в её состав:
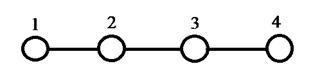
Рис. 10. Граф молекулы бутадиена.
На основании данных о молекулярном графе и виде топологической матрицы (или матрицы смежности), передающих информацию о молекулярной структуре сопряжённых и ароматических соединений, с учётом введенного орбитального параметра 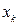 :
:
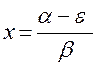
составим хюккелевский детерминант, порядок которого очевидно будет равен общему числу атомов углерода в молекуле:
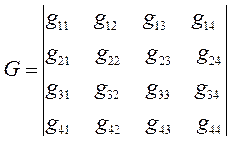
Полагая значения диагональных матричных элементов равными 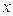 и далее, присваивая значения 1 тем недиагональным матричным элементам, которые соответствуют соседним атомам (между которыми имеет место химическая связь) и нуль тем недиагональным матричным элементам, которые отвечают несоседним атомам (между которыми химической связи нет), приходим к выражению вида:
и далее, присваивая значения 1 тем недиагональным матричным элементам, которые соответствуют соседним атомам (между которыми имеет место химическая связь) и нуль тем недиагональным матричным элементам, которые отвечают несоседним атомам (между которыми химической связи нет), приходим к выражению вида:
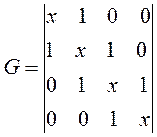
полученный таким образом детерминант приравнивают нулю, т.е. имеем:
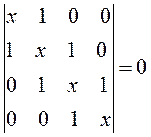
Для того чтобы раскрыть полученный в ходе проделанных выше выкладок определитель, используют самые различные подходы. Наиболее простой путь решения детерминанта такого типа является метод, основанный на получении общих решений, предложенный в своё время Ч. Коулсоном. Так, применительно к молекулам линейных полиенов – углеводородов с открытой цепью общей формулы 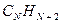 и чередующимися (альтернирующими) двойными и одинарными связями, хюккелевский детерминант как это было показано выше, будет иметь вид:
и чередующимися (альтернирующими) двойными и одинарными связями, хюккелевский детерминант как это было показано выше, будет иметь вид:
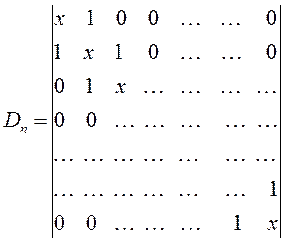
Понижение порядка детерминанта такого типа, когда число атомов углерода в молекуле полиена 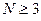 , производится по формуле:
, производится по формуле:
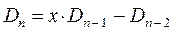
имеем:
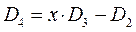
учитывая, что:
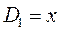
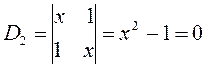
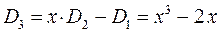
приходим для бутадиена к выражению вида:
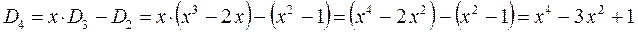
откуда следует соответственно, что:
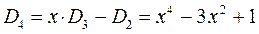
На основании общих решений векового детерминанта, рассчитаем значения орбитальных параметров, энергий и коэффициентов разложения для случая молекулы бутадиена:
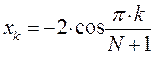
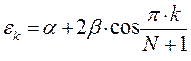
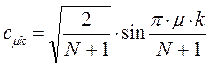
здесь 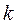 - индекс молекулярной орбитали,
- индекс молекулярной орбитали, 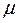 - индекс атомной орбитали и величина
- индекс атомной орбитали и величина 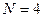 есть число атомов углерода в цепи сопряжения. Поскольку:
есть число атомов углерода в цепи сопряжения. Поскольку:
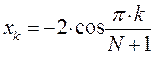
тогда после подстановки соответствующих величин, будем иметь:
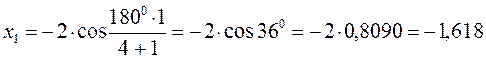
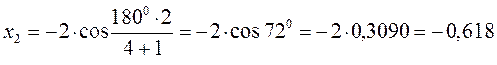
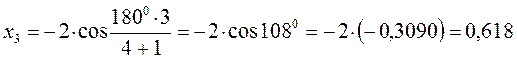
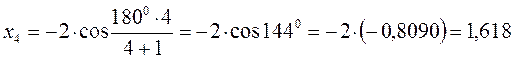
поскольку:
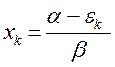
имеем:
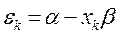
учитывая, что:
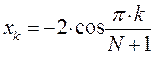
имеем:
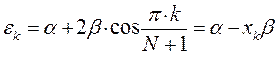
или после подстановки значений орбитальных параметров:
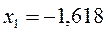 ;
; 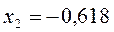 ;
; 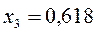 ;
; 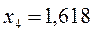
в уравнение вида:
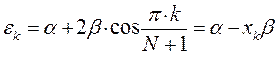
будем иметь соответственно:
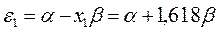
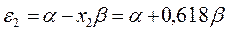
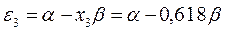
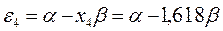
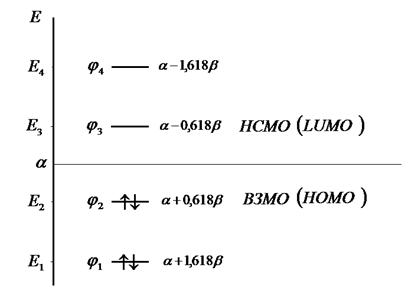
Рис.11. Диаграмма энергетических уровней молекулы
бутадиена (основное состояние)
На основании выражения вида:
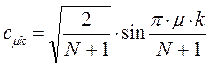
рассчитаем теперь значения орбитальных коэффициентов и построим аналитические выражения для связывающей и разрыхляющей молекулярных орбиталей бутадиена. Учитывая, разложение молекулярной орбитали 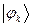 по базисному набору соответствующих атомных орбиталей
по базисному набору соответствующих атомных орбиталей 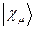 :
:
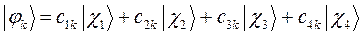
где 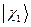 ,
, 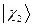 ,
, 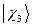 и
и 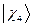 - атомные
- атомные 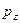 - орбитали слэйтеровского типа. Учитывая также, что
- орбитали слэйтеровского типа. Учитывая также, что 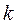 - индекс молекулярной орбитали,
- индекс молекулярной орбитали, 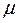 - индекс атомной орбитали и величина
- индекс атомной орбитали и величина 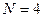 есть число атомов углерода в цепи сопряжения. Рассчитаем орбитальные коэффициенты для самой низкой в энергетическом отношении молекулярной орбитали
есть число атомов углерода в цепи сопряжения. Рассчитаем орбитальные коэффициенты для самой низкой в энергетическом отношении молекулярной орбитали 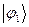 , в результате будем иметь соответственно:
, в результате будем иметь соответственно:
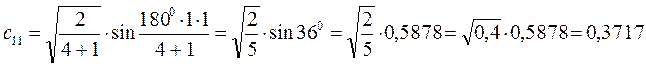
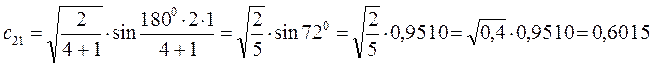
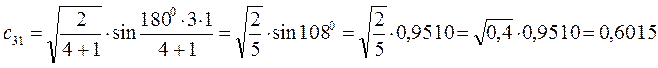
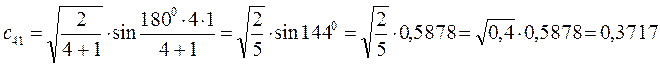
Рассчитаем теперь орбитальные коэффициенты для молекулярной орбитали 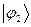 , в результате будем иметь соответственно:
, в результате будем иметь соответственно:
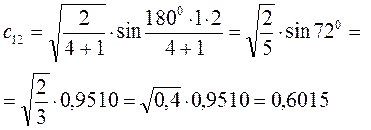
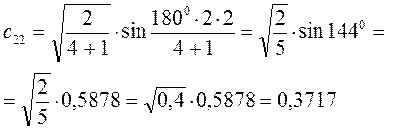
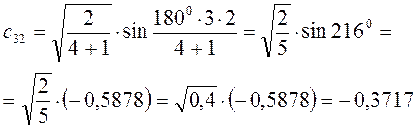
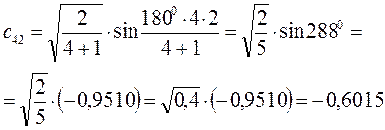
Рассчитаем теперь орбитальные коэффициенты для молекулярной орбитали 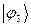 , в результате будем иметь соответственно:
, в результате будем иметь соответственно:
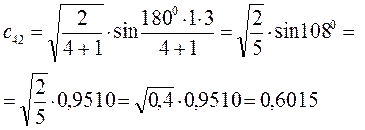
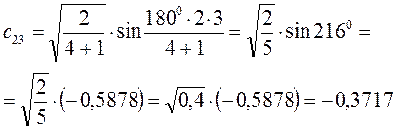
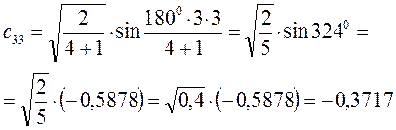
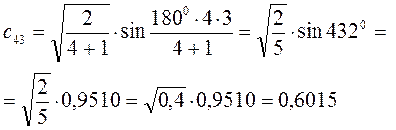
Рассчитаем теперь орбитальные коэффициенты для молекулярной орбитали 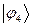 , в результате будем иметь соответственно:
, в результате будем иметь соответственно:
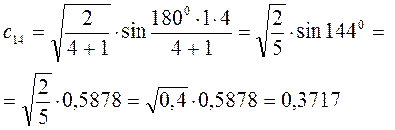
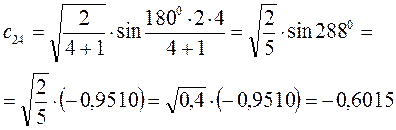
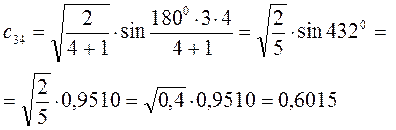
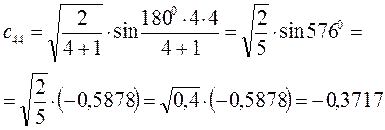
Таким образом, в ходе проделанных выкладок, приходим к выражениям для энергий и соответствующих им волновых функций связывающего и разрыхляющего состояний, полученных в ходе решения хюккелевского детерминанта 4-го порядка:
Таблица 10. Энергии связывающей и разрыхляющей молекулярных орбиталей молекулы бутадиена.
| Симметрия МО | Орбитальный параметр, 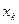 | Энергия МО, 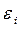 | МО, 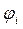 |
 | 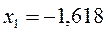 | 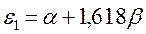 | 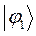 |
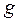 | 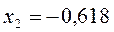 | 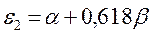 | 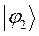 |
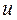 | 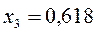 | 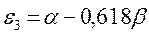 | 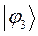 |
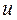 | 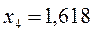 | 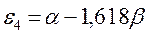 | 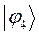 |
Таблица 11. Значения орбитальных коэффициентов.
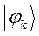 | 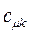 | 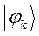 | 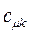 |
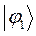 | 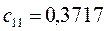 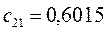 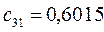 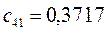 | 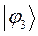 | 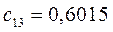 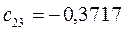 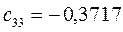 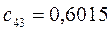 |
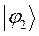 | 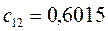 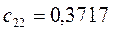 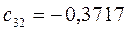 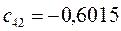 | 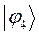 | 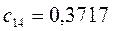 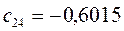 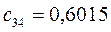 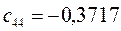 |
Поскольку:
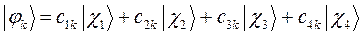
тогда с учётом полученных выше значений для коэффициентов разложения 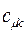 , будем иметь соответственно выражения для волновых функций связывающего и разрыхляющего состояний:
, будем иметь соответственно выражения для волновых функций связывающего и разрыхляющего состояний:
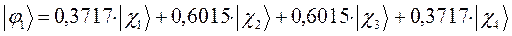
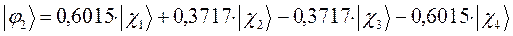
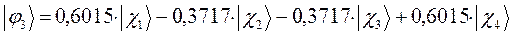
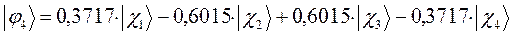
 2015-03-22
2015-03-22 1632
1632
