Классификация гипотез по областям их использования

Существующие статистические гипотезы очень многообразны; их количество продолжает увеличиваться и в настоящее время по мере развития математической статистики и её технических приложений. Одна из возможных схем классификации статистических гипотез представлена на рис. 7.3. Она не охватывает всех существующих статистических гипотез, но характеризуется стройной структурой. Это обусловлено её логичной связью с градацией математической статистики на области одномерной, многомерной статистики и статистики временных рядов (см. § 1.2). Соответственно этой градации выделяют несколько основных видов статистических гипотез, которые, в свою очередь, делятся на различные подвиды.

Гипотезы для одномерных выборок в первую очередь делятся в зависимости от закона распределения генеральных совокупностей и рассматриваемых выборок. Если закон распределения известен (обычно в технике априори принимается нормальное распределение), то используются гипотезы, основанные на «параметрических» критериях. Если закон распределения генеральных совокупностей неизвестен, то используются «непараметрические» критерии (представлены на рис. 7.3 лишь частично). В этих критериях часто рассматриваются не сами значения случайных величин X и Y, а лишь соотношения между ними X > Y, X < Y. Эти критерии особенно применимы для «порядковых» или «номинальных» случайных величин, о законах распределения которых вообще бессмысленно говорить.

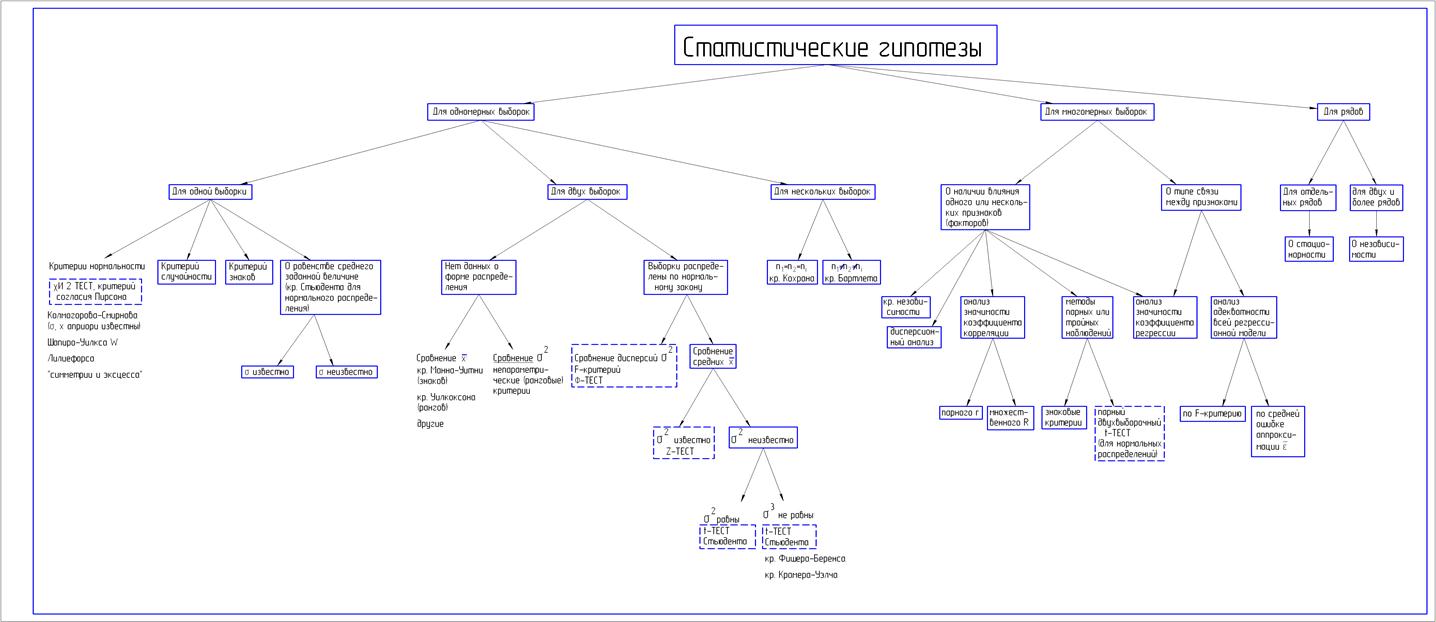
Рис. 7.3. Обзорная схема статистических гипотез

Гипотезы для одномерных выборок в зависимости от количества рассматриваемых выборок делятся на три категории (см. рис. 7.3):

- гипотезы для одной выборки;

- гипотезы для двух выборок;

- гипотезы для трёх и более выборок.

Для каждой отдельной выборки могут быть гипотезы, направленные на решение следующих задач:

- по проверке закона распределения;

- по установлению случайности выборки;

- касающиеся положения среднего, его равенства заданной величине;

- касающиеся попадания значения (единичного или среднего) в заданный интервал (на схеме рис. 7.3 не представлены).

Применительно к гипотезам для двух или нескольких одномерных выборок необходимо ввести понятие «однородности выборок». Если выборки однородны, то можно сделать заключение, что они относятся к одной генеральной совокупности.

Гипотезы для двух одномерных выборок можно разделить на два типа:

- гипотезы для выборок, нормальное распределение которых априори известно,

- гипотезы для выборок, нормальное распределение которых неизвестно.

Для обоснования однородности требуется осуществить проверку двух гипотез:

- что не обнаружено статистически значимых различий в величине их дисперсий,

- что не обнаружено статистически значимых различий в величине их средних значений.

Гипотезы для трёх и более одномерных выборок. Для обоснования однородности всех рассматриваемых выборок также требуется осуществить проверку отсутствия статистически значимых различий в величине дисперсий и проверку отсутствия статистически значимых различий в величине их средних значений. Проверка гипотезы о равенстве дисперсий трёх и более одномерных выборок рассмотрена в § 7.3.2, а сравнение средних значений нескольких выборок может быть сведено к проверке статистической значимости различие между двумя наиболее «проблемными» средними. Если значимого различия между двумя наиболее «проблемными» средними не обнаружено (см. § 7.3), тем более незначимо различие между остальными средними. Задача здесь состоит в правильном выборе наиболее «проблемной» пары выборок: это должна быть пара не только с сильно различающимися средними, но и с относительно малыми дисперсиями, т.к. величина дисперсий определяет статистическую значимость различия средних (см. § 7.4).

Б. Гипотезы для многомерных выборок, признаков, факторов, параметров, связанных с исследованиями связи между ними (данный раздел статистики [ ] здесь не представлен) можно разделить на два типа:

- гипотезы, определяющие наличие и степень достоверности связи одного признака с другим или с несколькими признаками (методы парных наблюдений, дисперсионный, корреляционный анализы),

- гипотезы, определяющие тип и форму связи одного признака с другими одним или с несколькими признаками (проверка коэффициентов регрессии по t - критерию, проверка коэффициента множественной корреляции).

В. Гипотезы для рядов также можно разделить на два типа:

- гипотезы для отдельного ряда (о стационарности),

- гипотезы для взаимодействия двух или нескольких рядов (о независимости).