Самым ярким представителем квантовых размерных эффектов является туннельный эффект – чисто квантовое явление, сыгравшее важную роль в развитии современной электронике и приборостроении. Феномен туннелирования был открыт в 1927 г. нашим соотечественником Г. А. Гамов, который впервые получил решения уравнения Шрёдингера, описывающие возможность преодоления частицей потенциального барьера, даже если её энергия меньше высоты барьера. Найденные решения помогли понять многие экспериментальные данные, которые невозможно было понять в рамках представлений классической физики.
Впервые в физике туннельный эффект был использован для объяснения радиоактивного 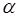 - распада атомных ядер, например:
- распада атомных ядер, например:
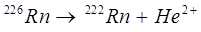
Дело в том, что 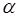 - частица – ядро атома гелия
- частица – ядро атома гелия 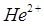 - не имеет достаточной энергии для того, чтобы покинуть нестабильное ядро. На этом пути
- не имеет достаточной энергии для того, чтобы покинуть нестабильное ядро. На этом пути 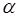 - частице необходимо преодолеть огромный (28 МэВ), но достаточно узкий (10-12 см – радиус ядра) потенциальный барьер. Советский учёный Г. Гамов (1927) показал, что распад атомного ядра в таком случае становится возможным именно за счёт тунелирования переноса
- частице необходимо преодолеть огромный (28 МэВ), но достаточно узкий (10-12 см – радиус ядра) потенциальный барьер. Советский учёный Г. Гамов (1927) показал, что распад атомного ядра в таком случае становится возможным именно за счёт тунелирования переноса 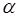 - частицы. Благодаря туннельному эффекту происходит также холодная эмиссия электронов из металлов и многие другие явления. Многие считают, что за грандиозность результатов его работ, ставших основополагающими для многих наук, Г.А. Гамов должен был быть удостоен нескольких Нобелевских премий. Лишь спустя тридцать лет после открытия Г. А. Гамова появились первые приборы на основе туннельного эффекта – туннельные диоды, транзисторы, датчики, термометры для измерения сверхнизких температур, и, наконец, сканирующие туннельные микроскопы, положившие начало современным исследованиям наноструктур. Туннельный эффект представляет собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелированный неизменной) меньше высоты барьера. Туннельный эффект – явление исключительно квантовой природы, которое не возможно было объяснить в рамках классических представлений. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда с точки зрения геометрической оптики, происходит полное внутреннее отражение. В общем случае, туннельный эффект представляет собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. В классической механике движение происходит при условии, что полная энергия частицы
- частицы. Благодаря туннельному эффекту происходит также холодная эмиссия электронов из металлов и многие другие явления. Многие считают, что за грандиозность результатов его работ, ставших основополагающими для многих наук, Г.А. Гамов должен был быть удостоен нескольких Нобелевских премий. Лишь спустя тридцать лет после открытия Г. А. Гамова появились первые приборы на основе туннельного эффекта – туннельные диоды, транзисторы, датчики, термометры для измерения сверхнизких температур, и, наконец, сканирующие туннельные микроскопы, положившие начало современным исследованиям наноструктур. Туннельный эффект представляет собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелированный неизменной) меньше высоты барьера. Туннельный эффект – явление исключительно квантовой природы, которое не возможно было объяснить в рамках классических представлений. Аналогом туннельного эффекта в волновой оптике может служить проникновение световой волны внутрь отражающей среды (на расстояния порядка длины световой волны) в условиях, когда с точки зрения геометрической оптики, происходит полное внутреннее отражение. В общем случае, туннельный эффект представляет собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелировании неизменной) меньше высоты барьера. В классической механике движение происходит при условии, что полная энергия частицы 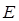 больше, чем её потенциальная энергия
больше, чем её потенциальная энергия 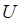 , т.е. имеет место неравенство:
, т.е. имеет место неравенство:
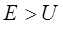
Поскольку полная энергия равна сумме кинетической и потенциальной энергий:
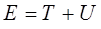
и кинетическая энергия больше нуля 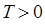 , то соответственно разность полной и потенциальной энергий, также будет больше нуля:
, то соответственно разность полной и потенциальной энергий, также будет больше нуля:
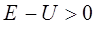
и таким образом будет выполняться условие вида:
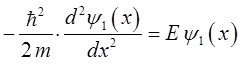
Необходимо отметить, что задача о движении частицы в потенциальном ящике удовлетворяет данному условию, поскольку внутри ящика потенциальная энергия равна нулю 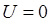 . Однако в квантовой механике движение возможно и при условии, когда полная энергия меньше потенциальной
. Однако в квантовой механике движение возможно и при условии, когда полная энергия меньше потенциальной 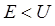 . Такие задачи объединяют общим названием – потенциальные барьеры. Рассмотрим потенциальный барьер прямоугольной формы. Пусть в области I
. Такие задачи объединяют общим названием – потенциальные барьеры. Рассмотрим потенциальный барьер прямоугольной формы. Пусть в области I 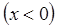 значение потенциала равно нулю,
значение потенциала равно нулю, 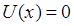 . В области II
. В области II 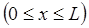 значение потенциальной энергии равно
значение потенциальной энергии равно 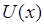 определяется высотой барьера
определяется высотой барьера 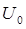 и таким образом
и таким образом 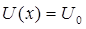 . В области III
. В области III 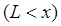 значение потенциальной энергии равно нулю,
значение потенциальной энергии равно нулю, 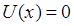 . Обозначим волновые функции для областей:
. Обозначим волновые функции для областей: 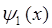 для области I,
для области I, 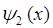 для области II и
для области II и 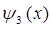 для области III. В данной задаче нас будет интересовать случай, когда полная энергия частицы меньше высоты потенциального барьера
для области III. В данной задаче нас будет интересовать случай, когда полная энергия частицы меньше высоты потенциального барьера 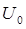 , т.е. при условии что
, т.е. при условии что 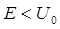 .
.
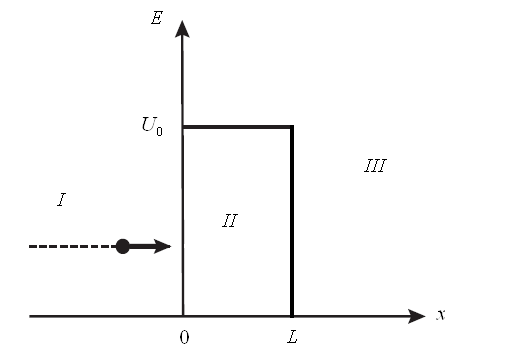
Рис.8. Прохождение частицы через потенциальный барьер
Для каждой из трёх областей запишем уравнение Шрёдингера, приведём его к стандартному виду и опишем его общие решения. Рассмотрим движение частицы в области I. Обозначим волновую функцию частицы в этом случае 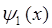 . Как и в случае свободного движения частицы, соответствующее уравнение Шрёдингера запишется в виде:
. Как и в случае свободного движения частицы, соответствующее уравнение Шрёдингера запишется в виде:
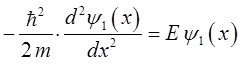
откуда следует, что:
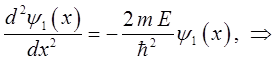
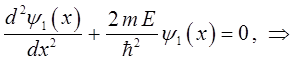
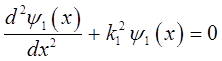
здесь:
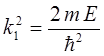
общее решение уравнения Шрёдингера для области I, может быть записано в виде:
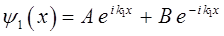
первую часть функции 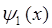 можно интерпретировать как падающую на потенциальный барьер волну (движение частицы слева направо в области I). Коэффициенты
можно интерпретировать как падающую на потенциальный барьер волну (движение частицы слева направо в области I). Коэффициенты 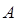 и
и 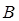 называют амплитудами соответственно падающей и отражённой волны. Они определяют вероятность прохождения волны через потенциальный барьер, а также вероятность её отражения от барьера. Поскольку коэффициенты разложения в выражении для волновой функции
называют амплитудами соответственно падающей и отражённой волны. Они определяют вероятность прохождения волны через потенциальный барьер, а также вероятность её отражения от барьера. Поскольку коэффициенты разложения в выражении для волновой функции 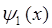 связаны с интенсивностью пучка частиц движущихся к барьеру или отражённых от него, тогда соответственно принимая амплитуду падающей волны
связаны с интенсивностью пучка частиц движущихся к барьеру или отражённых от него, тогда соответственно принимая амплитуду падающей волны 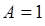 , будем иметь:
, будем иметь:
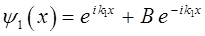
Рассмотрим теперь движение частицы в области II. В условиях данной задачи, физический интерес для нас будет представлять случай, когда полная энергия частицы меньше высоты потенциального барьера, что отвечает выполнению условия вида:
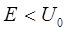
поскольку для области II:
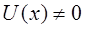
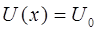
т.е. значения потенциальной энергии частицы определяется высотой барьера – размером области:
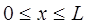
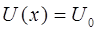
тогда уравнение Шрёдингера для области II будет иметь вид:
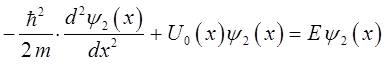
откуда следует, что:
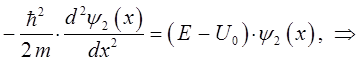
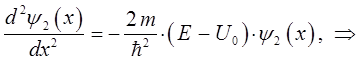
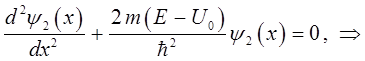
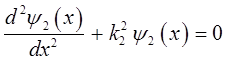
здесь:
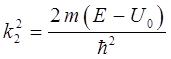
общее решение уравнения Шрёдингера для области II имеет вид:
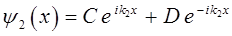
здесь первую часть функции 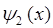 можно интерпретировать как прошедшую в область II волну с амплитудой
можно интерпретировать как прошедшую в область II волну с амплитудой 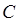 , а вторую часть – как волну, отражённую в области II с амплитудой
, а вторую часть – как волну, отражённую в области II с амплитудой 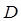 . Рассмотрим теперь движение частицы в области III. Учитывая свободный характер движения частицы в этой области и условия вида:
. Рассмотрим теперь движение частицы в области III. Учитывая свободный характер движения частицы в этой области и условия вида:
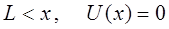
запишем и решим уравнение Шрёдингера для этой области, обозначив волновую функцию в виде - 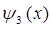 .
.
Имеем, таким образом, уравнение вида:
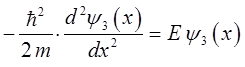
откуда следует, что:
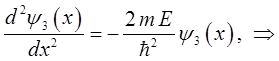
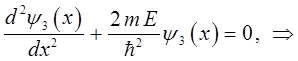
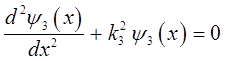
здесь:
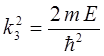
общее решение такого уравнения для области III, будет иметь вид:
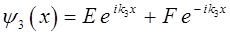
как и в предыдущих случаях, первую часть функции 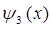 будем рассматривать как прошедшую в область III волну с амплитудой
будем рассматривать как прошедшую в область III волну с амплитудой 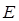 , а вторую часть решения – как отражённую в этой области волну с амплитудой
, а вторую часть решения – как отражённую в этой области волну с амплитудой 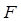 . Однако последнее является абсурдным с физической точки зрения, поскольку в области III имеется только волна, прошедшая сквозь потенциальный барьер и распространяющаяся в этой области слева направо. По этой причине коэффициент
. Однако последнее является абсурдным с физической точки зрения, поскольку в области III имеется только волна, прошедшая сквозь потенциальный барьер и распространяющаяся в этой области слева направо. По этой причине коэффициент 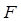 следует принять равным нулю
следует принять равным нулю 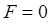 и общее решение уравнения Шрёдингера, описывающее движение частицы в области III, будет иметь вид:
и общее решение уравнения Шрёдингера, описывающее движение частицы в области III, будет иметь вид:
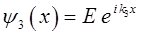
результаты приведенных выше выкладок сведём в соответствующую таблицу.
Таблица 2. Результаты расчёта
| Область квантования | Аналитические выражения |
Область I 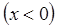 | 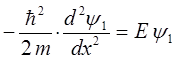 |
Область II 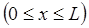 | 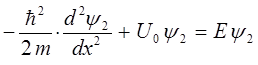 |
Область III 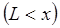 | 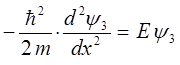 |
Область I 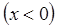 | 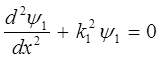 |
Область II 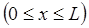 | 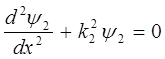 |
Область III 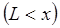 | 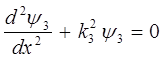 |
Область I 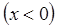 | 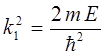 |
Область II 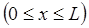 | 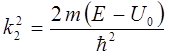 |
Область III 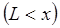 | 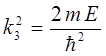 |
Область I 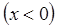 | 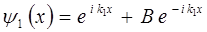 |
Область II 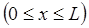 | 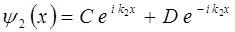 |
Область III 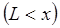 | 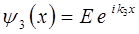 |
Область I 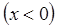 | 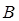 - амплитуда отражённой волны - амплитуда отражённой волны |
Область II 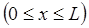 | 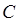 - амплитуда волны, прошедшей в область II - амплитуда волны, прошедшей в область II 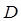 - амплитуда волны, отражённой в области II - амплитуда волны, отражённой в области II |
Область III 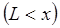 | 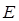 - амплитуда волны, прошедшей в область III - амплитуда волны, прошедшей в область III |
Амплитуды 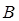 ,
, 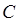 ,
, 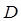 и
и 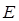 находим из условия «сшивки» волновых функций и их первых производных:
находим из условия «сшивки» волновых функций и их первых производных:
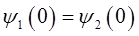
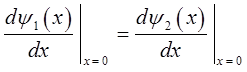
и аналогично:
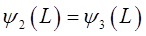
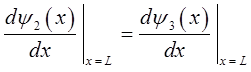
Подставляя в приведенные выше условия сшивки конкретные выражения для волновых функций:
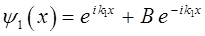
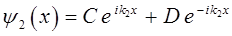
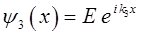
для первого условия сшивки волновых функций 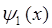 и
и 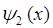 :
:
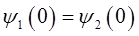
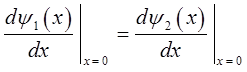
будем иметь соответственно:
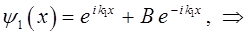
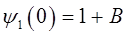
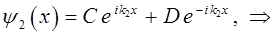
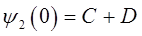
поэтому:
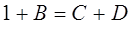
используя значения волновых функций 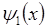 и
и 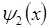 , найдём значения первых производных от этих функций:
, найдём значения первых производных от этих функций:
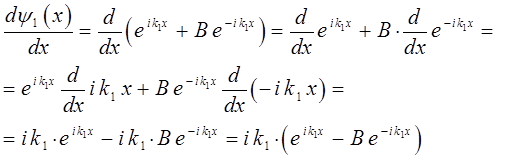
аналогично вычисляем:
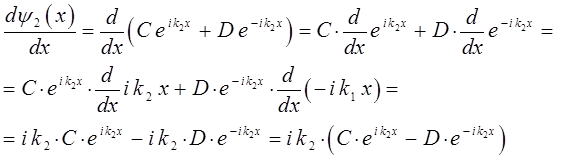
таким образом, имеем:
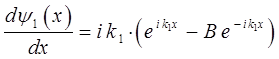
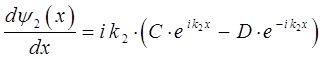
учитывая, что:
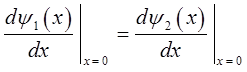
имеем:
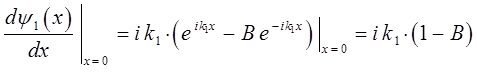
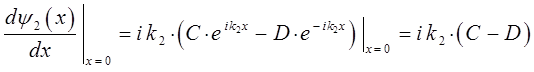
откуда следует, что:
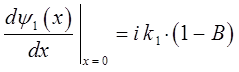
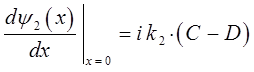
таким образом, имеем:
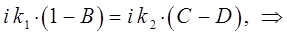
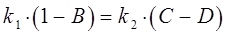
Из второго условия сшивки волновых функций:
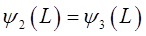
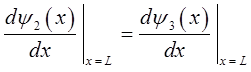
находим:
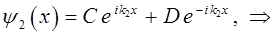
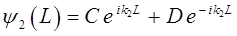
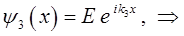
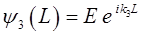
поэтому:
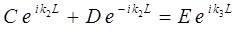
Используя значения волновых функций 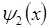 и
и 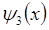 , найдём значения первых производных от этих функций:
, найдём значения первых производных от этих функций:
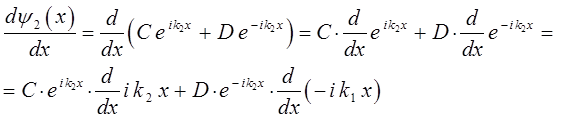
или в окончательном виде:
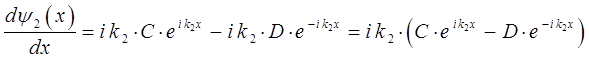
аналогично вычисляем:
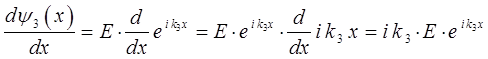
таким образом, имеем:
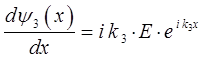
учитывая, что:
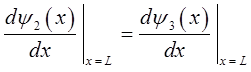
имеем:
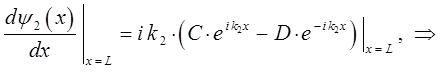
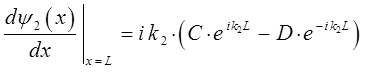
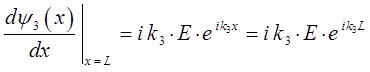
откуда следует, что:
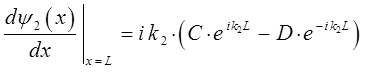
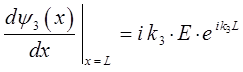
исходя из условия сшивки соответствующих волновых функций и равенства первых производных от функций 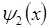 и
и 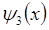 :
:
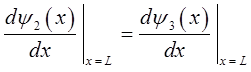
будем иметь соответственно:
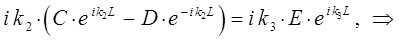
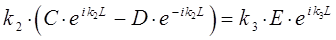
Подстановка конкретных выражений для волновых функций 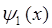 ,
, 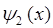 и
и 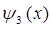 , и вычисление соответствующих производных входящих в условия сшивки для этих функций, приводит к следующей системе линейных относительно амплитуд
, и вычисление соответствующих производных входящих в условия сшивки для этих функций, приводит к следующей системе линейных относительно амплитуд 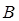 ,
, 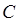 ,
, 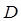 и
и 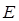 уравнений:
уравнений:
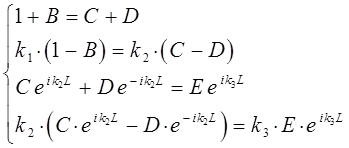
преобразуем полученную систему уравнений к виду:
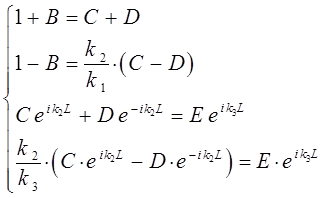
Решая полученную систему уравнений, линейных относительно амплитуд 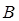 ,
, 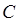 ,
, 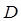 и
и 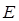 , не трудно получить выражения для каждой из них. Однако наиболее важным из получаемых решений данной системы, является получение выражения для амплитуды
, не трудно получить выражения для каждой из них. Однако наиболее важным из получаемых решений данной системы, является получение выражения для амплитуды 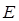 , характеризующей движение частицы в области III, которая как это хорошо видно из ниже приведенного выражения – отлична от нуля:
, характеризующей движение частицы в области III, которая как это хорошо видно из ниже приведенного выражения – отлична от нуля:
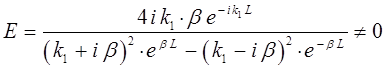
в полученном выражении для амплитуды 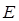 имеем:
имеем:
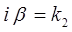
где вещественная величина 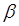 , входящая в выражение мнимой величины
, входящая в выражение мнимой величины 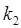 равна:
равна:
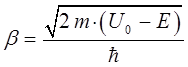
Получение отличной от нуля амплитуды 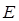 , характеризующей движение частицы в области III означает, что микрочастица с некоторой вероятностью может преодолеть потенциальный барьер, несмотря на то, что её энергия может быть меньше высоты такого барьера. Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, представляющему собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелированный неизменной) меньше высоты барьера. Туннельный эффект – явление исключительно квантовой природы, которое не возможно было объяснить в рамках классических представлений. Благодаря туннельному эффекту происходит также холодная эмиссия электронов из металлов и многие другие явления. Процессы туннельного переноса в химии интересны для относительно тяжёлых частиц. Как известно, на пути превращения реагентов в продукты имеется потенциальный барьер. При высоких температурах (при соответствующей активации реагентов) превращения проходят над барьером,
, характеризующей движение частицы в области III означает, что микрочастица с некоторой вероятностью может преодолеть потенциальный барьер, несмотря на то, что её энергия может быть меньше высоты такого барьера. Таким образом, квантовая механика приводит к принципиально новому специфическому квантовому явлению, получившему название туннельного эффекта, представляющему собой процесс преодоления микрочастицей потенциального барьера в случае, когда её полная энергия (остающаяся при туннелированный неизменной) меньше высоты барьера. Туннельный эффект – явление исключительно квантовой природы, которое не возможно было объяснить в рамках классических представлений. Благодаря туннельному эффекту происходит также холодная эмиссия электронов из металлов и многие другие явления. Процессы туннельного переноса в химии интересны для относительно тяжёлых частиц. Как известно, на пути превращения реагентов в продукты имеется потенциальный барьер. При высоких температурах (при соответствующей активации реагентов) превращения проходят над барьером, 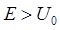 . Однако при низких температурах (часто в твёрдом состоянии) химические процессы могут протекать лишь по механизму туннельного переноса (через барьер),
. Однако при низких температурах (часто в твёрдом состоянии) химические процессы могут протекать лишь по механизму туннельного переноса (через барьер), 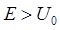 .
.
Для описания туннельного эффекта используют понятие коэффициента прозрачности 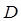 потенциального барьера, т.е. имеем:
потенциального барьера, т.е. имеем:
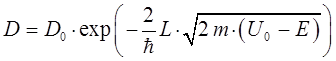
здесь предэкспоненциальный множитель 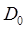 меняется сравнительно медленно с изменением высоты и ширины барьера, поэтому:
меняется сравнительно медленно с изменением высоты и ширины барьера, поэтому:
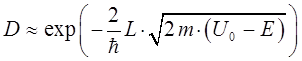
Таким образом, коэффициент прозрачности 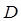 характеризует процессы прохождения частицы сквозь потенциальный барьер при условии
характеризует процессы прохождения частицы сквозь потенциальный барьер при условии 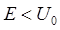 .
.
Он определяется запасом потенциальной энергии туннелируемой частицы и зависит от массы частицы. В общем случае, для туннельного переноса частицы через потенциальный барьер, необходимо, чтобы значение для 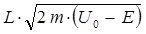 было сравнимо с величиной действия
было сравнимо с величиной действия 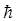 . Если значением
. Если значением 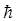 можно пренебречь, оказываются применимыми законы классической механики, согласно которым величина
можно пренебречь, оказываются применимыми законы классической механики, согласно которым величина 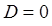 . Очевидно, что чем выше потенциальный барьер и шире, т.е. чем больше
. Очевидно, что чем выше потенциальный барьер и шире, т.е. чем больше 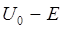 и соответственно больше величина
и соответственно больше величина 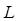 , тем меньше коэффициент прозрачности
, тем меньше коэффициент прозрачности 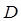 . Необходимо отметить, что в квантовой электродинамике, коэффициент прозрачности
. Необходимо отметить, что в квантовой электродинамике, коэффициент прозрачности 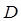 представляет собой отношение величины тока прошедшей волны к току падающей волны.
представляет собой отношение величины тока прошедшей волны к току падающей волны.
 2015-03-22
2015-03-22 9455
9455
