Матрица 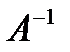 называется обратной матрице A, если выполняется условие
называется обратной матрице A, если выполняется условие 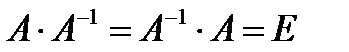 , где Е — единичная матрица того же порядка, что и матрица a. Матрица
, где Е — единичная матрица того же порядка, что и матрица a. Матрица 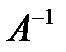 имеет те же размеры, что и матрица A.
имеет те же размеры, что и матрица A.
Теорема. Всякая невырожденная матрица имеет обратную.

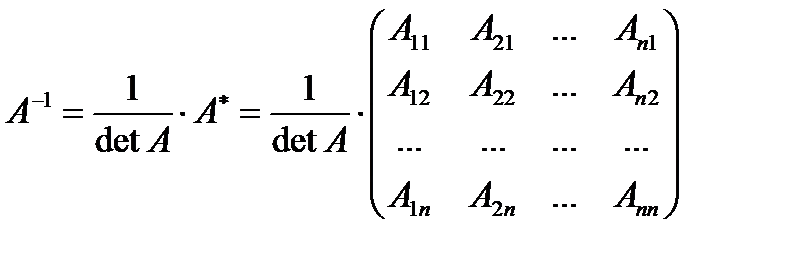 , где
, где 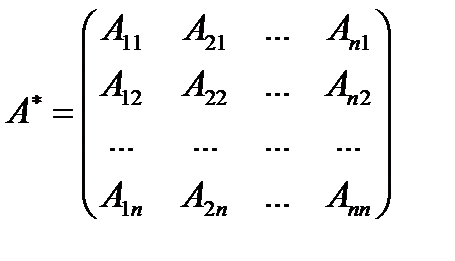 - матрица, союзная к матрице А и где Aij — алгебраические дополнения элемента
- матрица, союзная к матрице А и где Aij — алгебраические дополнения элемента 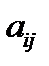 данной матрицы А
данной матрицы А
Пример. Найти 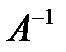 , если
, если 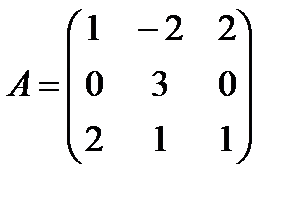
1) Находим 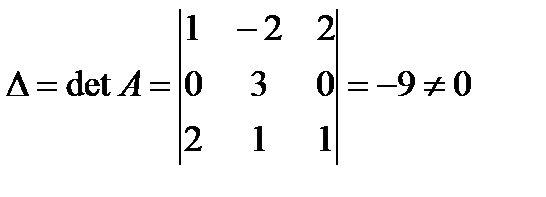
2) Находим  :
: 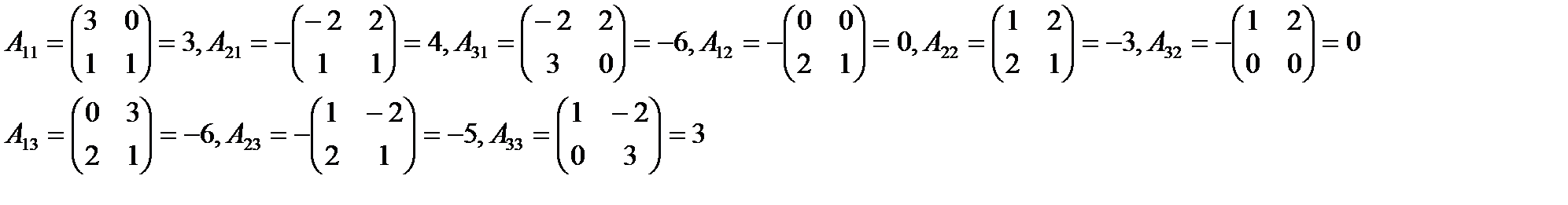 ,
,
поэтому 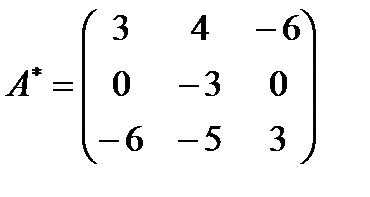
3) Находим 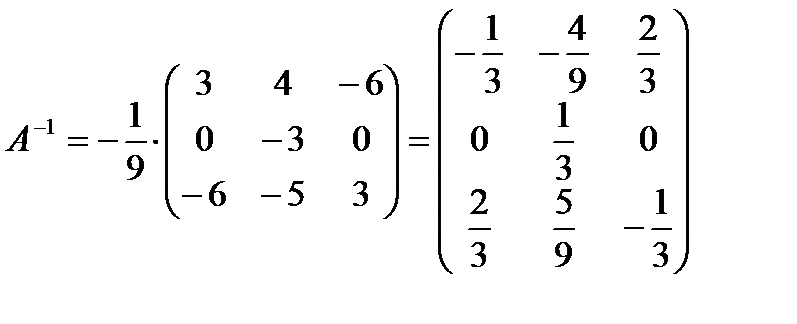
4) Проверка: 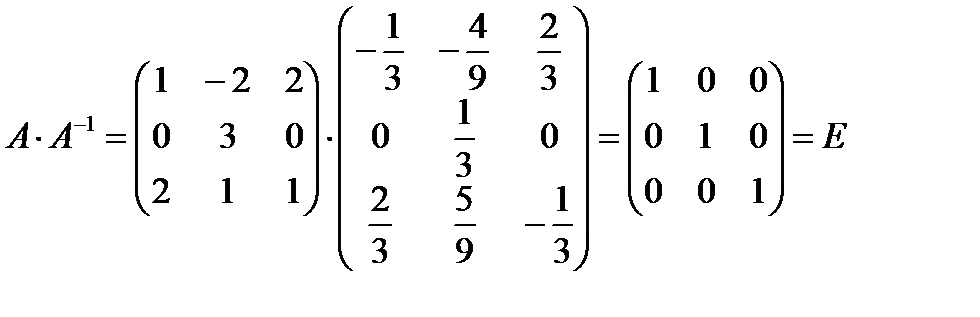
 2015-03-22
2015-03-22 521
521








