Одним из наиболее универсальных и эффективных методов решений линейных алгебраических систем является метод Гаусса, состоящий в последовательном исключении неизвестных.
Пусть дана система уравнений
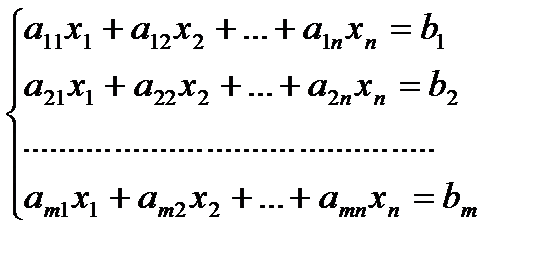 (*)
(*)
Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому (в частности, треугольному) виду.
Приведенная ниже система имеет ступенчатый вид
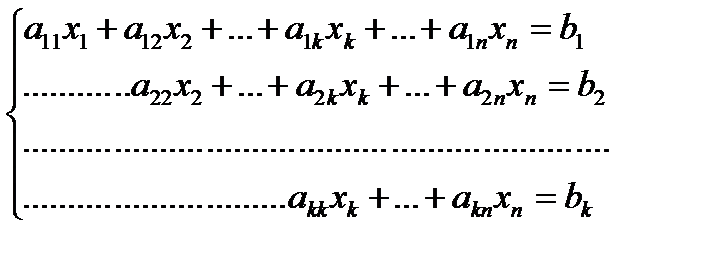
где 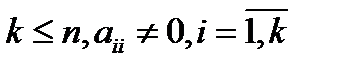 . Коэффициенты
. Коэффициенты 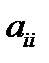 называются главными элементами системы.
называются главными элементами системы.
На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.
Опишем метод Гаусса подробнее.
Прямой ход.
Будем считать, что элемент  (если
(если 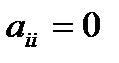 , то первым в системе запишем уравнение, в котором коэффициент при
, то первым в системе запишем уравнение, в котором коэффициент при 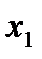 отличен от нуля).
отличен от нуля).
Преобразуем систему (*), исключив неизвестное 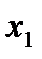 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на
во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на 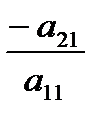 и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на
и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на 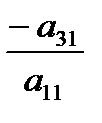 и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
и сложим с третьим уравнением системы. Продолжая этот процесс, получим эквивалентную систему
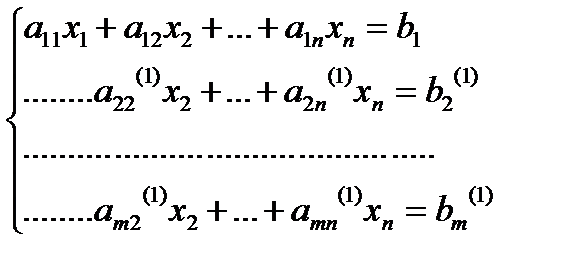
Здесь 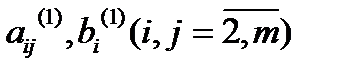 — новые значения коэффициентов и правых частей, которые получаются после первого шага.
— новые значения коэффициентов и правых частей, которые получаются после первого шага.
Аналогичным образом, считая главным элементом 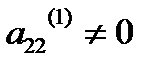 , исключим неизвестное х2 из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
, исключим неизвестное х2 из всех уравнений системы, кроме первого и второго, и так далее. Продолжаем этот процесс, пока это возможно.
Если в процессе приведения системы (*) к ступенчатому виду появятся нулевые уравнения, т. е. равенства вида 0 = 0, их отбрасывают. Если же появится уравнение вида 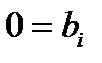 ,а
,а 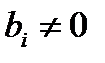 , то это свидетельствует о несовместности системы.
, то это свидетельствует о несовместности системы.
Второй этап (обратный ход) заключается в решении ступенчатой системы. Ступенчатая система уравнений, вообще говоря, имеет бесчисленное множество решений. В последнем уравнении этой системы выражаем первое неизвестное 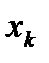 через остальные неизвестные
через остальные неизвестные 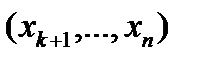 . Затем подставляем значение
. Затем подставляем значение 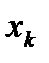 в предпоследнее уравнение системы и выражаем
в предпоследнее уравнение системы и выражаем 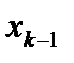 через
через 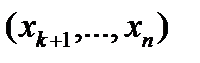 , затем находим
, затем находим 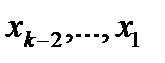 . Придавая свободным неизвестным
. Придавая свободным неизвестным 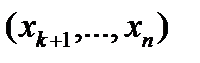 произвольные значения, получим бесчисленное множество решений системы.
произвольные значения, получим бесчисленное множество решений системы.
Замечания:1. Если ступенчатая система оказывается треугольной, т.е. 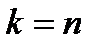 , то исходная система имеет единственное решение. Из последнего уравнения находим
, то исходная система имеет единственное решение. Из последнего уравнения находим 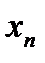 , из предпоследнего уравнения
, из предпоследнего уравнения 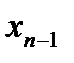 , далее поднимаясь по системе вверх, найдем все остальные неизвестные
, далее поднимаясь по системе вверх, найдем все остальные неизвестные 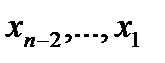 .
.
2. На практике удобнее работать не с системой (*), а с расширенной ее матрицей, выполняя все элементарные преобразования над ее строками. Удобно, чтобы коэффициент 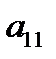 был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на
был равен 1 (уравнения переставить местами, либо разделить обе части уравнения на 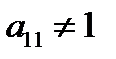 ).
).
Пример 4. Решить систему методом Гаусса:
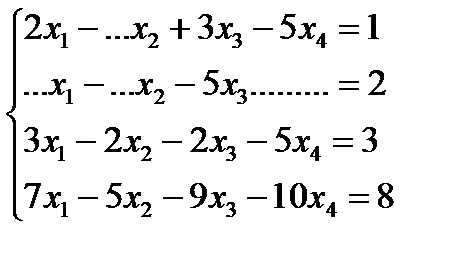
Решение: В результате элементарных преобразований над расширенной матрицей системы
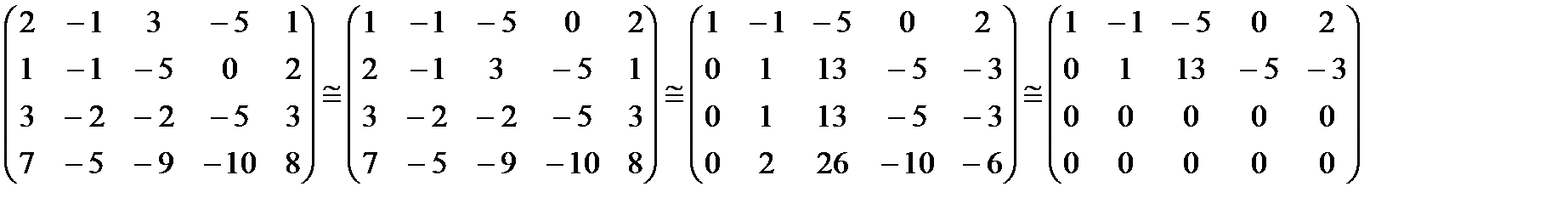
исходная система свелась к ступенчатой:
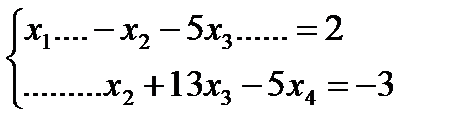
Поэтому общее решение системы: 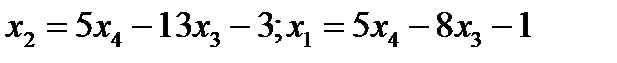 . Если положить, например,
. Если положить, например, 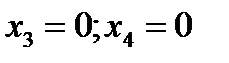 , то найдем одно из частных решений этой системы
, то найдем одно из частных решений этой системы 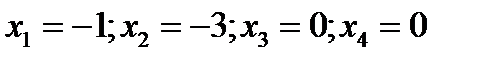 .
.
 2015-03-22
2015-03-22 1228
1228
