2015-03-22
1410
Пусть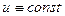 
. В этом случае решение дифференциального уравнения, соответствующее установившейся составляющей переходного процесса, ищется в виде 
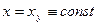. Так как 
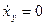, то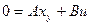 
.
При условии, что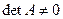 
(т.е.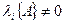 
), алгебраическое уравнение 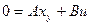единственным образом разрешимо относительно 
:
.
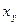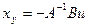Подставляя найденное решение в уравнение выхода, находим статическую характеристику системы
.
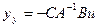Принимая во внимание выражение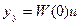 
, очевидно равенство 
.
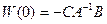Если система такова, что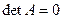 
, то матрица A необратима, и система не имеет статического режима.
