II ДВОИЧНАЯ АРИФМЕТИКА
Арифметические операции с числами в двоичной системе счисления
Пример. Найти сумму двоичных дробных чисел 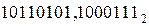 и
и 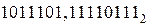 .
.
Решение.
| [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] | |||
| + | 1, | 02 | ||||||||||||||
| 1, | 12 | |||||||||||||||
| 1, | 12 |
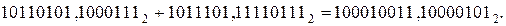
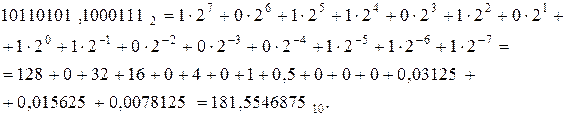
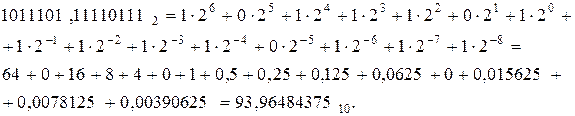
181,554687510+93,9648437510=275,5195312510.
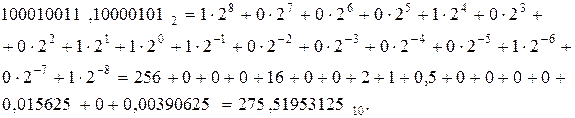
Пример. Найти разность двоичных дробных чисел 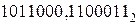 и
и 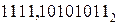 .
.
Решение.
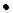
| 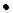
| [1] | [1] | 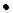
| [1] | [1] | 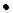
| 
|  заёмы из старших разрядов заёмы из старших разрядов
| ||||||||
| - | 0, | 12 |  уменьшаемое уменьшаемое
| ||||||||||||||
| 1, | 12 |  вычитаемое вычитаемое
| |||||||||||||||
| 1, | 12 |  разность разность
|
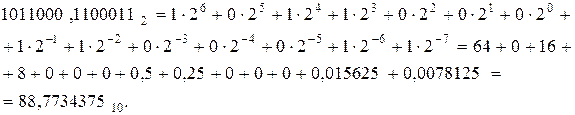
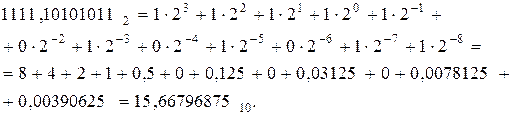
88,773437510-15,667968710=73,1054687510.
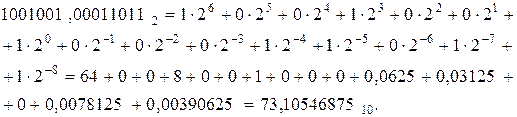
При умножении двух двоичных дробных чисел необходимо придерживаться следующих трёх правил:
- числа перемножаются без учета запятых;
-
- в полученном произведении запятая ставится так, чтобы отделить справа столько же знаков, сколько отделено в обоих множителях вместе взятых.
Пример.
Найти произведение двоичных дробных чисел 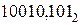 и
и 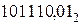 .
.
Решение. Операция нахождения произведения указанных дробных двоичных чисел требует выполнения сложений неполных произведений, что в свою очередь требует проведения большого количества переносов в старшие разряды. Для повышения наглядности пронумеруем разряды и приведем результаты поразрядных сложений.
| 0, | 12 |  множимое множимое
| |||||||||||||||
| 0, | 12 |  множитель множитель
| ||||||||||||||||
| [1] | [1] | [1] | [1] | [1] | [1] | [1] | [1] |  переносы в старшие разряды переносы в старшие разряды
| ||||||||||
| + | 
|  неполные произведения неполные произведения
| ||||||||||||||||
| + | ||||||||||||||||||
| + | ||||||||||||||||||
| + | ||||||||||||||||||
| 1, | 12 | 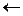 результат операции произведения результат операции произведения
|
Поразрядное сложение неполных произведений (строки 4 по 8) подробно описано ниже:
| 0 разряд = 1; | ||
| 1 разряд = 0; | ||
| 2 разряд = 1; | ||
| 3 разряд = 0+1=1; | ||
| 4 разряд = 1+0+1=10 (0 пишем в 4 разряде, 1 переносим в 5 разряд [1]); | ||
| 5 разряд=[+1]+0+1+0+1=11 (1 пишем в 5 разряде, 1 переносим в 6 разряд [1]); | ||
| 6 разряд = [+1]+0+0+1+0=10; | ||
| 7 разряд = [+1]+1+1+0+1+1=101 (1 пишем в 7 разряде, 0 переносим в 8 разряд, 1 переносим в 9 разряд [1]); | ||
| 8 разряд =0+1+0+0=1; | ||
| 9 разряд = [1]+0+0+1+1=11; | ||
| 10 разряд = [1]+1+0+0+0=10; | ||
| 11 разряд = [1]+1+0+1=11; | ||
| 12 разряд = [1]+1+0=10; | ||
| 13 разряд = [1]+0=1; | ||
| 14 разряд = 1. |
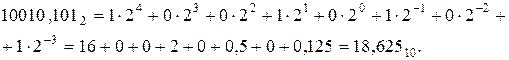
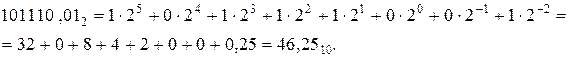
 2015-03-22
2015-03-22 393
393







