2015-03-22
391
Найти частное двоичных дробных чисел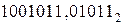 
и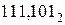 
с точностью до пяти знаков после запятой.
| [1] | [1] |
| |||||||||||||||||||
| - | 0, | 12 | 12 | |||||||||||||||||||
| 1, | 02 | |||||||||||||||||||||
|
|
|
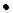
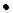
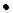
| [1] |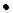
| ||||||||||||||||||
| - | ||||||||||||||||||||||
|
|
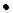
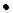
| [1] |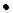
| |||||||||||||||||||
| - | ||||||||||||||||||||||
|
| ||||||||||||||||||||||
| - | ||||||||||||||||||||||
|
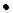
| [1] | [1] | [1] | [1] | [1] | |||||||||||||||||
| - | ||||||||||||||||||||||
|
|
|
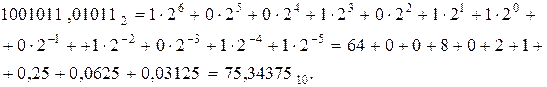
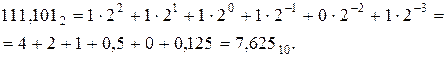
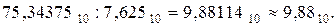
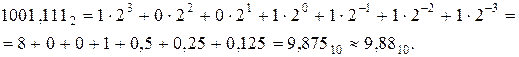
Общая формула представления числа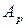 
в развернутой форме записи в позиционной системе счисления с основанием 
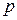, имеет вид:
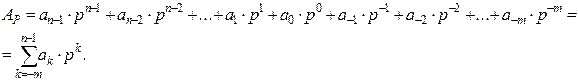
| (1) |
где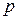 
- основание системы счисления числа 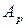, состоящего из 
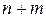разрядов (
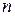разрядов целой части и 
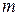разрядов дробной части); 
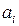- цифра целой части числа 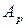, отстоящая на 
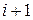позиций от запятой влево, 
; 
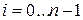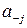- цифра дробной части числа 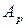, отстоящая на 
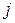позиций от запятой вправо, 
; 
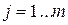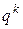− вес цифры числа .
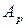Как видно из (1), развернутая форма записи числа равна сумме произведений каждой цифры числа на соответствующий ее вес цифры.
Из одной системы счисления в другую могут быть переведены, как целые, так и дробные числа. На первый взгляд, такой перевод кажется ординарным, однако для компьютерной техники это далеко непростая задача, так как связана с архитектурой компьютера. Трудность составляет размещение периодических и непериодических дробей, так как ресурсы компьютера не бесконечны. Решением проблемы является округление дробей и задание класса точности чисел, участвующих в вычислениях и появляющихся в их результате.
|
|
|
