Определение: Если Х независимая переменная, то дифференциал функции f(x) наз. f’(x)Dx=u обозначают df(x).
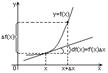
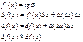
Теорема об инвариантной форме первого дифференциала.
df(x)=f’(x)dx
Доказательство:
1).
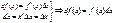
2). 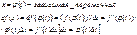
Производная высших порядков.
Определение: Производная второго порядка называется производная производной данной функции:
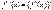
Определение: Производная n-го порядка называется производной производной n-1-го порядка.
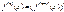
Пример:
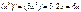
Используя метод математической индукции несложно показать, что:
1). n-ая производная обладает свойством линейности, т.е.:
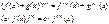
2). 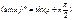
3). 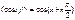
4). 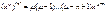
5). 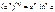
6). 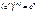
Дифференцирование функций заданных параметрически.
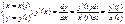
Пример 1:
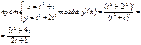 возьмем t=1, тогда x=2, y=3; y’(2)=7/3
возьмем t=1, тогда x=2, y=3; y’(2)=7/3
Пример 2:
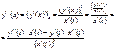
 2015-03-22
2015-03-22 411
411








