Постановка задачи. Общий вид нелинейного уравнения можно представить следующим образом

Общий вид нелинейного уравнения можно представить следующим образом:

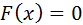(1)

Где функция 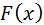определена и непрерывна на конечном или бесконечном интервале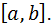

Определение: Всякое число 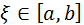, обращающее функцию 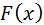в нуль, называется корнем уравнения (1).

Определение: Число 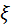называется корнем k -ой кратности, если при 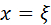вместе с функцией 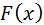равны нулю ее производные до 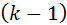-го порядка включительно:

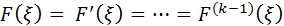(2)

Определение: Однократный корень называется простым.

Определение: Уравнение 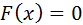и 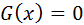называются равносильными (эквивалентными), если множества решений данных уравнений совпадают.

Нелинейные уравнения с одной переменной подразделяются на алгебраические и трансцендентные.

Определение: Уравнение (1) называется алгебраическим, если функция 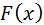является алгебраической.

Путем алгебраических преобразований из всякого алгебраического уравнения можно получить уравнение в канонической форме:

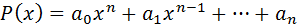(3)

где 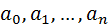- действительные коэффициенты уравнения; 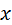- неизвестное.

Всякое алгебраическое уравнение имеет, по крайней мере, один вещественный или два комплексно сопряженных корня.

Определение: Уравнение (1) называется трансцендентным, если функция 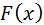не является алгебраической.

Определение: Решить уравнение (1) означает следующее:

1. Установить имеет ли уравнение корни.

2. Определить число корней уравнения.

3. Найти значения корней уравнения с заданной точностью.