2015-03-22
243
В мире всё относительно
и, прежде всего, отношения.
Абу Али аль-Хавои.
Определение 1. Два элемента одного или разных множеств, расположенные в определенном порядке, называется упорядоченной парой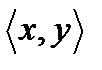 
.
Определение 2. Две упорядоченные пары 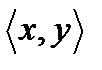и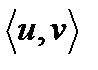 
равны, если 
.
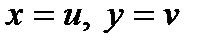Замечание. Естественно,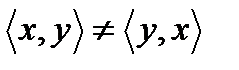 
, если 
.
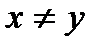Замечание. Упорядоченная n-ка (читается энка):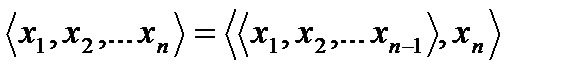 
.
Определение 3. Декартовым (прямым) произведением множеств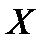 
и 
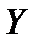(обозначается 
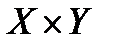) называется множество всех упорядоченных пар 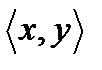таких, что 
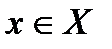, а 
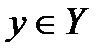. Множество 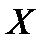часто называют множеством прообразов, а множество 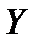– множеством образов.
Определение 4. Любое подмножество декартова произведения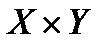 
называется бинарным отношением 
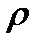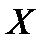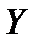между множеством и (обозначается 
).
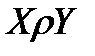Среди бинарных отношений важнейшим является функция (от лат. functio – исполнение).
Определение 5. Пусть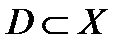 
, а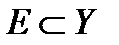 
.Подмножество 
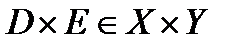декартова произведения множеств 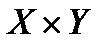называется функцией, если 
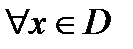есть парный элемент точно одной пары 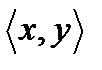. Обозначается 
.
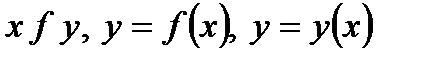Определение 5*. Если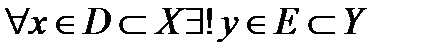 
, то такое отношение и его результат называется функцией. Множество 
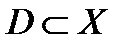называется областью определения функции, а множество 
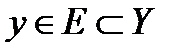– областью изменения функции; 
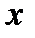называют аргументом (от лат. functio - действовать), 
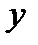– значением функции.
Определение 6. Функция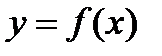 
называется инъективной, если 
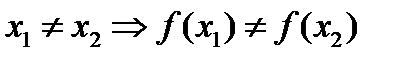, то есть каждому 
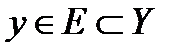соответствует не более одного 
.
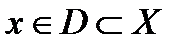Определение 7. Функция 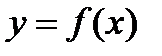называется сюръективной, если 
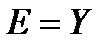, то есть каждому 
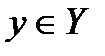соответствует, по крайней мере, один .
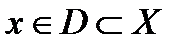Определение 8. Функция 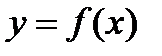называется биективной, если она и инъективна и сюръективна, т.е. 
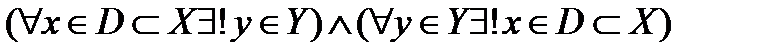. Так как в этом случае каждому 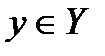соответствует единственный 
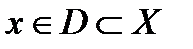, то существует функция 
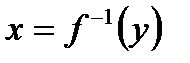, которая называется обратной по отношению к функции (
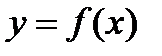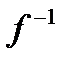– обозначение обратной функции).
