Глава I Множества. Логика
Грядущие поколения будут
рассматривать теорию множеств
как болезнь, от которой они излечились.
А. Пуанкаре, 1908 год
Определение 1. “Множество – совокупность элементов, обладающих определенными свойствами и связанных между собой или элементами других множеств определёнными отношениями ” (Н. Бурбаки).
Замечание. Подчёркнутые слова не определяются.
Замечание. “Множество есть многое, мыслимое как единое целое” (Г. Кантор – основатель теории множеств).
Определение 2. Задать множество – указать точное правило, с помощью которого о любом элементе можно сказать: является ли он элементом данного множества. Это можно сделать перечислением (для конечных множеств) или указанием характеристического свойства 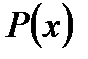 , т.е. такого свойства, которым обладают все элементы задаваемого множества и не обладают никакие элементы никаких других множеств. Обычно множество выделяется из более общего множества, которое называется UNIVERSUM (вселенная) и обозначается буквой U.
, т.е. такого свойства, которым обладают все элементы задаваемого множества и не обладают никакие элементы никаких других множеств. Обычно множество выделяется из более общего множества, которое называется UNIVERSUM (вселенная) и обозначается буквой U.
Пример. Множество 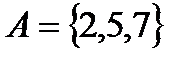 – множество, заданное перечислением; множество
– множество, заданное перечислением; множество 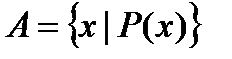 – множество элементов
– множество элементов 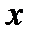 , заданное правилом
, заданное правилом 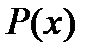 . Например,
. Например, 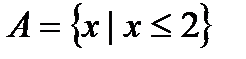 – множество тех, и только тех действительных
– множество тех, и только тех действительных  , которые не больше двух.
, которые не больше двух.
На универсуме U множества обозначаются кругами, которые называются кругами Эйлера. Множества обозначаются большими буквами латинского алфавита, элементы – соответствующими маленькими (рис.1).
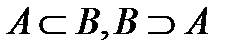


| Рис.1Hhhfghfutu6uu1111111111111111111 |
Знак 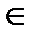 означает принадлежность и применяется для элементов,
означает принадлежность и применяется для элементов, 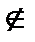 – не принадлежать,
– не принадлежать, 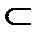 – принадлежать для множеств. Множество, не содержащее ни одного элемента, называется пустым и обозначается
– принадлежать для множеств. Множество, не содержащее ни одного элемента, называется пустым и обозначается 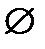 .
.
Определение 3. Два множества называются равными, если они состоят из одних и тех же элементов. Обозначается 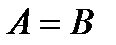 .
.
Пример. 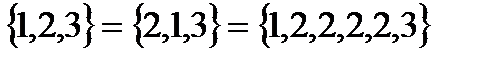 ; но
; но 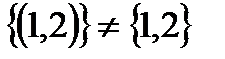 , так как единственным элементом множества
, так как единственным элементом множества 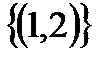 является упорядоченная пара
является упорядоченная пара 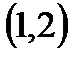 , а множество
, а множество 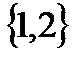 состоит из двух элементов: 1 и 2.
состоит из двух элементов: 1 и 2.
Определение 4. Множество 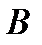 есть подмножество множества
есть подмножество множества 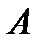 , если
, если 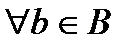 справедливо
справедливо 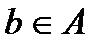 . Обозначается:
. Обозначается: 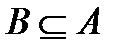 . Говорят, что множество
. Говорят, что множество 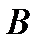 строго включено во множество
строго включено во множество 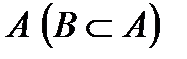 , если
, если 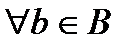 справедливо, что
справедливо, что 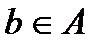 , но
, но 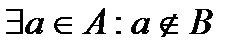 .
.
Определение 5. 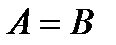 , если
, если 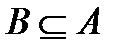 и
и 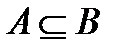 (т.е. они состоят из одних и тех же элементов).
(т.е. они состоят из одних и тех же элементов).
Пример. 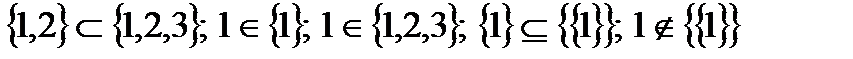 , так как единственным элементом множества
, так как единственным элементом множества 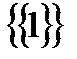 является множество
является множество 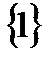 .
.
Определение 6. Рассмотрим множество всех подмножеств конечного множества 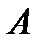 и обозначим его
и обозначим его 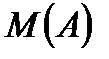 . Таким образом,
. Таким образом, 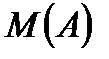 содержит пустое множество
содержит пустое множество 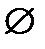 и само множество
и само множество 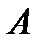 . Эти подмножества называются несобственными, а остальные собственными (собственно говоря, они и есть нетривиальные подмножества).
. Эти подмножества называются несобственными, а остальные собственными (собственно говоря, они и есть нетривиальные подмножества).
Пример. Пусть 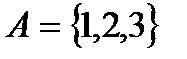 , тогда
, тогда 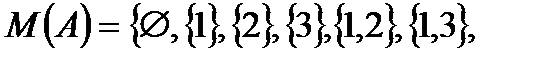
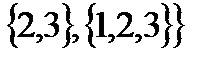 .
.

| Рис. 2 |
 и
и 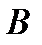 (
(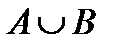 (читается
(читается 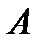 чашка
чашка 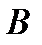 ) называется новое множество
) называется новое множество 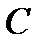 , элементами которого являются элементы множества
, элементами которого являются элементы множества 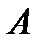 или элементы множества
или элементы множества 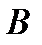 :
: 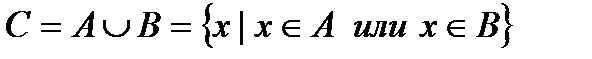 (рис.2). Слово “или” употребляется в неразделительном смысле и обозначается значком
(рис.2). Слово “или” употребляется в неразделительном смысле и обозначается значком  , который называется “ дизъюнкция ” (от лат. disjunctio – разобщение, различие). Тогда
, который называется “ дизъюнкция ” (от лат. disjunctio – разобщение, различие). Тогда 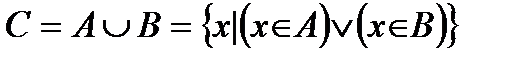 .
.
Аналогично даются определения остальных операций над множествами. Мы их просто выпишем.
Определение 
| Рис. 3 |
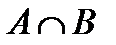 (читается
(читается 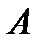 крышка
крышка 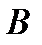 ).
).
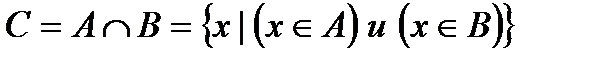 (рис.3). Слово “и” обычно заменяют значком
(рис.3). Слово “и” обычно заменяют значком  - “конъюнкция” (от лат. conjunctio – союз, связь), и тогда множество
- “конъюнкция” (от лат. conjunctio – союз, связь), и тогда множество 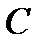 описывается так:
описывается так: 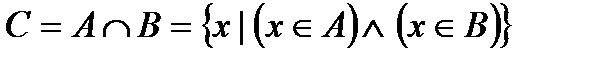 .
.

| Рис. 4 |
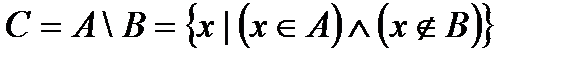 (рис. 4) - все те элементы множества
(рис. 4) - все те элементы множества 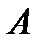 , которые не являются элементами множества
, которые не являются элементами множества 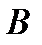 .
.

| Рис. 5 |
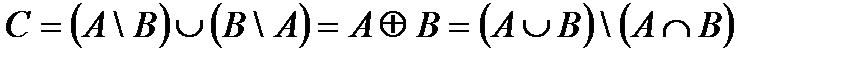 (рис.5).
(рис.5).

| Рис.6 |
Определение 11. Дополнением множества 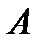 до универсума называется множество, состоящее из всех тех элементов универсума, которые не являются элементами множества
до универсума называется множество, состоящее из всех тех элементов универсума, которые не являются элементами множества 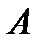 (рис. 6). Обозначают
(рис. 6). Обозначают 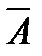 .
.
Определение 12. Характеристической функцией множества 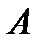 называется функция
называется функция 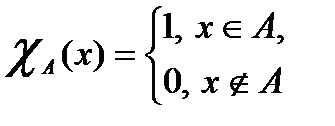 .
.
Легко составить характеристические функции для всех перечисленных операций. Они называются таблицами Буля. С их помощью легко доказываются свойства операций над множествами.
| U | 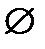
| 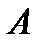
| 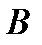
| 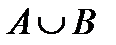
| 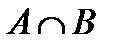
| 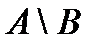
| 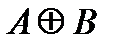
| |||||||||
 2015-03-22
2015-03-22 373
373







