РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПРИ НЕСИНУСОИДАЛЬНЫХ ПЕРИОДИЧЕСКИХ Э.Д.С., НАПРЯЖЕНИЯХ И ТОКАХ
При потреблении электрической энергии в большом числе практически важных случаев необходимо поддерживать синусоидальность токов, напряжений и э.д.с. Реальные э.д.с., напряжения и токи, оставаясь периодическими функциями времени, в той или иной мере отличаются от синусоидальных. Основными причинами этого являются:
· несовершенство конструкций генераторов и другого оборудования электрических станций,
· наличие нагрузок (потребителей энергии), эквивалентные параметры которых зависят от приложенных к ним напряжений и протекающих по ним токов, то есть нелинейных нагрузок.
Указанные причины приводят к изменению формы кривых тока и напряжения. Кроме того, в цепи могут действовать источники, генерирующие периодические последовательности импульсов различной формы. Такие задачи являются характерными при анализе процессов в электронных цепях.
Несинусоидальные э.д.с., напряжения и токи
Периодические напряжения, токи и э.д.с. можно представить в виде рядов Фурье, которые в общем случае содержат постоянную составляющую, основную (первую) гармонику, имеющую период, равный периоду самой функции, и высшие гармоники, частота которых в целое число раз больше частоты первой гармоники.
Например, для периодической э.д.с. можем записать
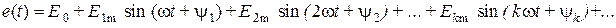
Здесь: 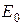 - постоянная составляющая э.д.с.;
- постоянная составляющая э.д.с.; 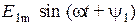 - основная (первая гармоника);
- основная (первая гармоника); 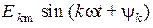 - высшая гармоника порядка
- высшая гармоника порядка 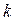 (
(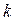 -ая гармоника),
-ая гармоника), 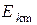 - амплитуда и
- амплитуда и 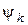 - начальная фаза
- начальная фаза 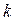 -ой гармоники.
-ой гармоники.
Заметим, что разложение в ряд Фурье возможно для функций, удовлетворяющих условиям Дирихле, которым всегда подчиняются э.д.с., напряжения и токи в реальных электрических цепях.
Представив члены ряда Фурье через синусы и косинусы без начальных фаз
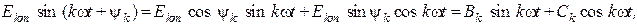 можно записать ряд Фурье в виде:
можно записать ряд Фурье в виде:
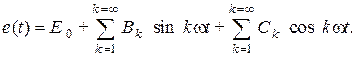
Константа 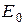 и коэффициенты
и коэффициенты 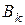 и
и 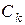 определяются соотношениями:
определяются соотношениями:
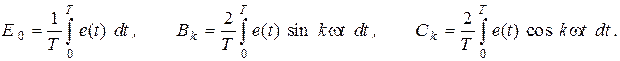
Располагая величинами 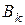 и
и 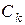 , нетрудно определить амплитуду и начальную фазу
, нетрудно определить амплитуду и начальную фазу 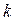 -ой гармоники:
-ой гармоники:
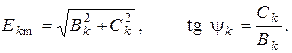
Аналогично можно разложить в ряд Фурье периодические несинусоидальные токи и напряжения.
Амплитуды 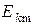 и начальные фазы
и начальные фазы 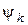 в зависимости от аргумента
в зависимости от аргумента 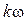 можно рассматривать как дискретные спектры функции
можно рассматривать как дискретные спектры функции 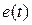 . Дискретные спектры удобно представлять в виде графиков. Для дискретных значений частот
. Дискретные спектры удобно представлять в виде графиков. Для дискретных значений частот 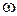 ,
, 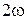 ,...,
,..., 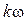 ,... параллельно оси ординат откладываются отрезки, длины которых пропорциональны амплитудам
,... параллельно оси ординат откладываются отрезки, длины которых пропорциональны амплитудам 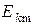 и начальным фазам
и начальным фазам 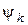 гармоник. При этом
гармоник. При этом 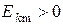 , а
, а 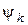 может принимать как положительные, так и отрицательные значения.
может принимать как положительные, так и отрицательные значения.
Зависимости указанного вида носят название соответственно дискретных амплитудо-частотной и фазо-частотной характеристик.
При наличии того или иного вида симметрии в кривых тока, напряжения, э.д.с. некоторые коэффициенты разложения в ряд Фурье обращаются в нуль.
Значительное число непериодических функций времени, встречающихся в практической электротехнике, удовлетворяют условию 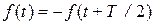 .
.
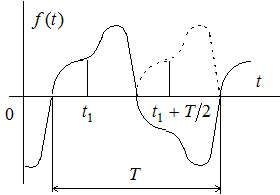 Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они представляются рядом Фурье, не содержащим постоянной составляющей и четных гармоник
Функции, удовлетворяющие этому условию, называются симметричными относительно оси абсцисс. Они представляются рядом Фурье, не содержащим постоянной составляющей и четных гармоник
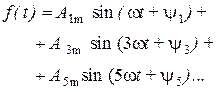
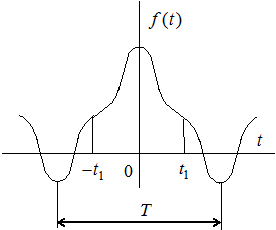 Функции, удовлетворяющие условию
Функции, удовлетворяющие условию 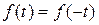 , то есть четные функции, симметричны относительно оси ординат.
, то есть четные функции, симметричны относительно оси ординат.
При этом 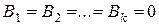 , и разложение в ряд Фурье имеет вид
, и разложение в ряд Фурье имеет вид
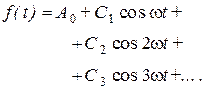
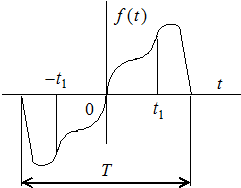 Если кривая симметрична относительно начала координат, т.е.
Если кривая симметрична относительно начала координат, т.е. 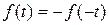 , имеем нечетную функцию.
, имеем нечетную функцию.
В этом случае
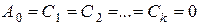 , и ряд Фурье запишется в виде
, и ряд Фурье запишется в виде
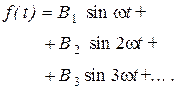
Отметим, что условие симметрии относительно оси абсцисс не зависит от выбора начала отсчета времени, т.е. является свойством самих кривых, тогда как остальные рассмотренные виды симметрии связаны с выбором начала отсчета времени.
Рассмотрим пример разложения периодической несинусоидальной функции, представляющей собой последовательность прямоугольных импульсов, в ряд Фурье.
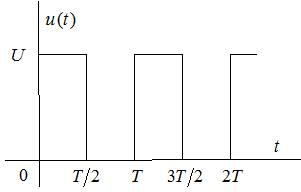
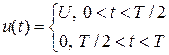
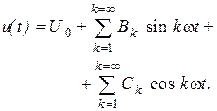
Коэффициенты разложения рассчитаем по приведенным выше формулам:
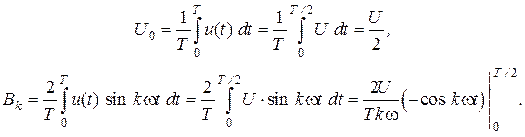
Учитывая, что 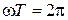 , получим
, получим
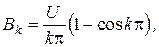
откуда при четных значениях 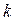 коэффициент
коэффициент 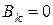 , а при нечетных
, а при нечетных 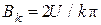 .
.
Аналогично для коэффициентов 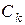 получим
получим
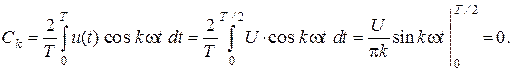
В результате можем записать
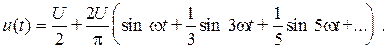
В общем случае разложение в ряд Фурье содержит бесконечное число членов, но в инженерных расчетах учитывается конечное число членов ряда.
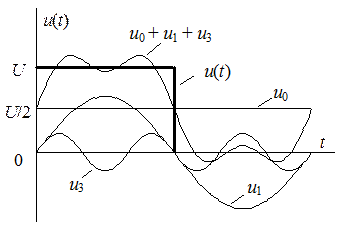
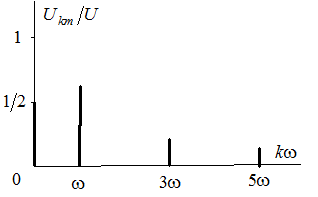
Ограничившись в рассматриваемом примере тремя членами ряда, изобразим на рисунке сумму постоянной составляющей, первой и третьей гармоник, а также дискретную амплитудо-частотную характеристику функции 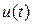 .
.
 2015-03-22
2015-03-22 624
624







