Дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
ay'' + by' + cy = f(x), (12.43)
где a, b, c - постоянные, f(x)- функция от х.
Если f(x)= 0, то уравнение (12.43) называется однородным дифференциальным уравнением с постоянными коэффициентами или уравнением без правой части:
ay'' + by' + cy = 0. (12.44)
Уравнение (12.44) можно привести к виду
y'' + py' + qy = 0. (12.45)
Уравнение k2 + pk + q = 0 (12.46)
называется характеристическим уравнением для уравнения (12.45).
В зависимости от корней k1 и k2 характеристического уравнения (12.46) получаем общее решение уравнения (12.45) в виде
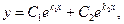 (12.47)
(12.47)
если k1 и k2 - различные действительные числа;
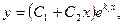 (12.48)
(12.48)
если k1 = k2;
y=eα x(C1cosβ x+C2sinβ x), (12.49)
если k1 = α+ iβ, k2 = α-iβ - комплексные числа.
1. Найти общее решение уравнения y'' - 5y' + 6y = 0 и выделить частное решение, удовлетворяющее начальным условием: y =1, y' = 2 при x=0.
Характеристическое уравнение (12.46) для данного уравнения принимает вид
k2 - 5k + 6 = 0.
Так как это уравнение имеет различные действительные корни k1 = 2, k2 = 3, то в соответствии с формулой (12.47) общее решение данного дифференциального уравнения таково:
y = C1e2x + C2e3x.
Чтобы найти искомое частное решение, подставим начальные данные в выражения для y и у', где
y' = 2C1e2x + 3C2e3x.
Подстановка этих данных приводит к системе уравнений:
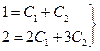
откуда определяются значения произвольных постоянных: C1 = 1, C2 = 0.
Следовательно, искомое частное решение определяется формулой
y = e2x.
2. Проинтегрировать уравнение y'' + 4y'+ 4y = 0.
Характеристическое уравнение k2 + 4k + 4 = 0 имеет равные корни k1 = k2 = - 2.
В соответствии с формулой (12.48) получаем общее решение исходного дифференциального уравнения
y = e-2x(C1 + C2x).
3. Проинтегрировать уравнение y'' + y' + y = 0.
Характеристическое уравнение k2 + k + 1 = 0
имеет комплексные корни
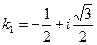
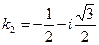
В соответствии с формулой (12.49) находим общее решение
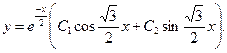
Найти общие решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами:
12.59. 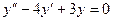
12.61. 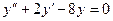
12.63. 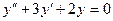
12.65. 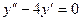
12.67. 12.58. 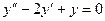
12.60. 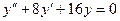
12.62. 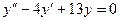
12.64. 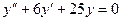
12.66. 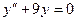
12.68. 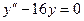
 2015-03-22
2015-03-22 1155
1155
