Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид
y'' + py' + qy = f(x). (12.50)
Общее решение уравнения находится по формуле
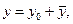 (12.51)
(12.51)
где y0 - решение соответствующего однородного уравнения
y'' + py' + qy = 0, (12.52)
а 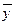 - частное решение неоднородного уравнения.
- частное решение неоднородного уравнения.
В простейших случаях, когда функция f(x), входящая в уравнение (12.50), является показательной или полиномом, указанное частное решение находится с помощью метода неопределенных коэффициентов.
Если f(x)=aemx, (12.53)
где a, m - постоянные, то частное решение уравнения (12.52) находится в виде
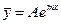 (12.54)
(12.54)
когда m не является корнем характеристического уравнения для уравнения (12.52), и в виде 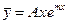 или
или 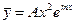 (12.55)
(12.55)
когда m - соответственно простой или кратный корень характеристического уравнения.
Если f(x)= a cos mx+b sin mx, (12.56)
где a, b, m - постоянные, то частное решение уравнения (12.50) ищут в виде
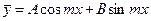 (12.57)
(12.57)
когда p2+(q-m2)2 ≠ 0, и в виде
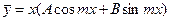 , (12.58)
, (12.58)
когда p = 0, q = m2.
Если f(x) = Pn(x), (12.59)
где Pn(x) - многочлен степени n, то частное решение уравнения (12.50) ищут в виде
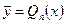 (12.60)
(12.60)
при q ≠ 0
и в виде 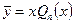 (12.61)
(12.61)
при q = 0, p ≠ 0.
1. Проинтегрировать уравнение y'' - 2y' + 2y = 6e2x .
Найдем сначала общее решение соответствующего однородного уравнения y'' - 2y' + 2y = 0.
Характеристическое уравнение k2 - 2k + 2 = 0 имеет комплексные
корни k1 = 1 + i, k2 = 1 - i. Следовательно, общее решение однородного уравнения таково:
y0=ex(C1cos x+C2sin x).
Находим частное решение исходного уравнения. Так как в данном случае
f(x) = 6e2x (т.е. f (x) = aemx, где a = 6, m = 2) и m = 2 не является корнем характеристического уравнения, то в соответствии с формулой (12.54) имеем частное решение в виде 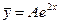 .
.
Находя производные этой функции 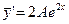 ,
, 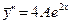 и подставляя выражения для y, y', y'' в исходное уравнение, получим
и подставляя выражения для y, y', y'' в исходное уравнение, получим
4Ae2x-2× 2Ae2x+2Ae2x = 6e2x, 2Ae2x = 6e2x.
Так как 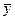 - решение уравнения, то последнее равенство выполняется для всех x, т.е. является тождеством, 2Ae2x≡6e2x, откуда 2A = 6, A = 3.
- решение уравнения, то последнее равенство выполняется для всех x, т.е. является тождеством, 2Ae2x≡6e2x, откуда 2A = 6, A = 3.
Следовательно, частное решение имеет вид 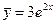 .
.
На основании формулы (12.51) получаем общее решение исходного уравнения
y=ex(C1cos x+C2sin x)+3e2x.
2. Найти общее решение уравнения
y'' + 3y' + 2y = 2x2- 4x -17.
Правая часть данного уравнения является полиномом второй степени f(x) = P2(x) = ax2 + bx + c, где a = 2, b = - 4, c = - 17.
Так как q ≠ 0, то в соответствии с формулой (12.60) частное решение ищем в виде 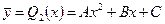
Подставляя выражения для 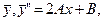
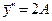
в данное уравнение, получаем
2Ax2+(6A+2B)x+(2A+3B+2C)=2x2-4x-17.
Поскольку 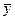 - решение дифференциального уравнения, то последнее равенство должно выполняться для всех x, т.е. является тождеством, поэтому коэффициенты при одинаковых степенях x, стоящие в разных частях, равны между собой:
- решение дифференциального уравнения, то последнее равенство должно выполняться для всех x, т.е. является тождеством, поэтому коэффициенты при одинаковых степенях x, стоящие в разных частях, равны между собой:
2A = 2, 6A + 2B = - 4, 2A + 3B + 2C = -17.
Из полученной системы уравнений находим, что A = 1, B = - 5, C = -2,
поэтому 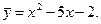 .
.
Общее решение соответствующего однородного уравнения
y'' + 3y' + 2y = 0
определяется формулой y0 = C1e-x+C2e-2x,
так как характеристическое уравнение k2 + 3k + 2 = 0 имеет корни
k1 = -1, k2 = - 2. На основании формулы (2) получаем общее решение
y = C1e-x+C2e-2x+x2-5x-2
исходного уравнения.
3. Проинтегрировать уравнение y'' + 4y' + 4y = 2sin 2x + 3cos 2x.
Правая часть данного уравнения является тригонометрическим
полиномом вида f(x) = a cos mx+ b sin mx, где a = 3, b = 2, m = 2.
Так как выполняется условие p2+(q-m2)2 ≠ 0, в соответствии с формулой (12.57) частное решение ищем в виде 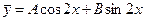 .
.
Находя производные 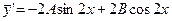 ,
, 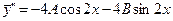
и подставляя в данное уравнение выражения для 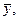
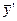 ,
, 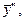 получим
получим
-4Acos 2x-4Bsin 2x+4(-2Asin 2x+2Bcos2x)+4 (Аcos2x+Bsin2x) ≡ 2sin2x+3cos2x
или
8Bcos 2x-8Asin2x ≡ 3cos2x+2sin2x,
откуда
8 B = 3, - 8 A = 2,т.е. 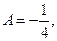
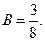
Следовательно, частное решение уравнения определяется формулой
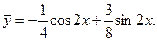
Соответствующее однородное уравнение y''+4y'+4y=0 имеет общее решение y0=(C1+C2x)e-2x.
По формуле (12.51) находим общее решение данного уравнения
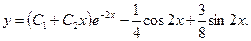
Найти общие решения уравнения:
12.69. 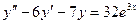
12.71. 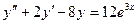
12.73. 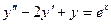
12.75. 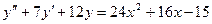
12.77 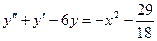
12.70. 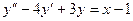
12.72. 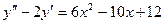
12.74. 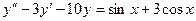
12.76. 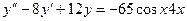
12.78. 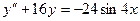
 2015-03-22
2015-03-22 994
994








