2015-03-22
266
1 метод: Получив выражение для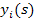 
, выполнить обратное преобразование Лапласа.
Выражение, полученное для 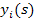, в правой части содержит только управляющие воздействия и возмущения, т.е. исходная система уравнений разделилась на отдельные выражения по координатам 
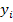. Этот метод называется операторным методом.
2 метод: Если от выражений, записанных в преобразованиях Лапласа, формально перейти к выражениям во временной области, заменяя произведения изображений по Лапласу свертками функций оригинала, получим выражение для 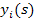в интегральной форме.
Для рассмотренной 2-мерной системы:
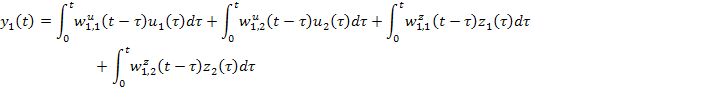
При определении временных характеристик обычно рассматривают реакции многосвязного объекта или системы на одно воздействие при фиксированных остальных.
3 метод: Решение системы дифференциальных уравнений Коши.
Задача в общем случае при произвольных порядках многочленов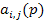 
достаточно сложная.
