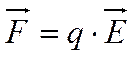 Отсюда сила, действующая на ряд q со стороны электрического поля, равна:
Отсюда сила, действующая на ряд q со стороны электрического поля, равна:
(2)
Направление вектора Е совпадает с направлением силы, действующей на положительный заряд, и противоположно направлению силы, действующей на отрицательный заряд.
Согласно формуле (1) напряженность поля в единицах СИ можно выразить в ньютонах на кулон (И/Кл).
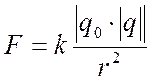 Напряженность поля точечного заряда. Найдем напряженность электрического поля, создаваемого точечным зарядом q0. По закону Кулона этот заряд будет действовать на другой заряд с силой, равной:
Напряженность поля точечного заряда. Найдем напряженность электрического поля, создаваемого точечным зарядом q0. По закону Кулона этот заряд будет действовать на другой заряд с силой, равной:
Модуль напряженности поля точечного заряда q0 на расстоянии rот него равен:
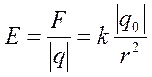 |
(3)
Вектор напряженности в любой точке электрического поля направлен вдоль прямой, соединяющей эту точку и заряд (рис1).
Принцип суперпозиции полей. Если на тело действует несколько сил, то согласно законам механики результирующая сила равна - геометрической сумме сил: 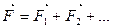 .
.
На электрические заряды действуют силы со стороны электрического поля. Если при наложении полей от нескольких зарядов эти поля не оказывают никакого влияния друг на друга, то результирующая сила со стороны всех полей должна быть равна геометрической сумме сил со стороны каждого поля. Опыт показывает, что именно так и происходит на самом деле. Это означает, что напряженности полей складываются геометрически.
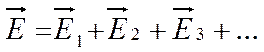 В этом состоит принцип суперпозиции полей, который формулируется так: если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых
В этом состоит принцип суперпозиции полей, который формулируется так: если в данной точке пространства различные заряженные частицы создают электрические поля, напряженности которых 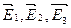 и т. д., то результирующая напряженность поля в этой точке равна:
и т. д., то результирующая напряженность поля в этой точке равна:
Благодаря принципу суперпозиции для нахождения напряженности поля системы заряженных частиц в любой точке достаточно знать выражение (3) для напряженности поля точечного заряда. На рисунке 2 показано, как определяется напряженность поля Е в точке А, созданная двумя точечными зарядами: q1 и q2
Введение электрического поля позволяет задачу вычисления сил взаимодействия заряженных частиц разбить на две части. Сначала вычисляют напряженность поля, созданного зарядами, а затем по известной напряженности определяют силы. Такое разделение задачи на части обычно облегчает расчеты сил.
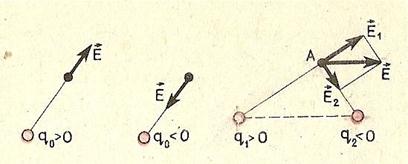 |
Рис.1 Рис.2
СИЛОВЫЕ ЛИНИИ ЭЛЕКТРИЧЕСКОГО ПОЛЯ. НАПРЯЖЕННОСТЬ ПОЛЯ ЗАРЯЖЕННОГО ШАРА.
Электрическое поле не действует на органы чувств. Его мы не видим. Тем не менее, распределение поля в пространстве можно сделать видимым. Делается это довольно просто.
Мы получим некоторое представление о распределении поля, если нарисуем векторы напряженности поля в нескольких точках пространства (рис. 1). Картина будет более наглядной, если нарисовать непрерывные линии, касательные к которым в каждой точке, через которую они проходят, совпадают с векторами напряженности. Эти линии называют силовыми линиями электрического поля или линиями напряженности (рис. 2).
Не следует напряженности думать, что линии - это существующие в действительности образования вроде растянутых упругих нитей или шнуров, как предполагал сам Фарадей. Линии напряженности помогают лишь наглядно представить распределение поля в пространстве и не более реальны, чем меридианы и параллели на земном шаре.
Однако силовые линии можно сделать видимыми. Если продолговатые кристаллики изолятора (например, хинина) хорошо перемешать в вязкой жидкости (например, в касторовом масле) и поместить туда заряженные тела, то вблизи этих тел кристаллики выстроятся в цепочки вдоль линии напряженности.
На рисунках приведены примеры линий напряженности: положительно заряженного шарика (рис. 3); двух разноименно заряженных шариков (рис. 4); двух одноименно заряженных шариков (рис. 5); двух пластин, заряды которых равны по модулю и противоположны по знаку (рис. 5). Последний пример особенно важен. На рисунке 6 видно, что в пространстве между пластинами ближе к середине силовые линии параллельны: электрическое поле здесь одинаково во всех точках.
Электрическое поле, напряженность которого одинакова во всех точках пространства, называется однородным. В ограниченной области пространства электрическое поле можно считать приблизительно однородным, если напряженность поля внутри этой области меняется незначительно.
Силовые линии электрического поля не замкнуты, они начинаются на положительных зарядах и оканчиваются на отрицательных. Силовые линии непрерывны и не пересекаются, так как пересечение означало бы отсутствие определенного направления напряженности электрического поля в данной точке. Они начинаются, или оканчиваются на заряженных телах, а затем расходятся в разные стороны (см. рис. 3). Поэтому густота силовых линий больше вблизи заряженных тел, где напряженность поля также больше.
Поле заряженного шара. Рассмотрим электрическое поле заряженного проводящего шара радиусом R. Заряд q равномерно распределен по поверхности шара. Силовые линии электрического поля, как вытекает из соображений симметрии, направлены вдоль продолжений радиусов шара (рис. 7 ). Обратите внимание! Силовые линии вне шара распределены в пространстве точно так же, как и силовые линии точечного заряда (рис. 8 ). Если совпадают картины силовых линий, то можно ожидать, что совпадают и напряженности полей. Поэтому на расстоянии r≥R от центра шара напряженность поля определяется той же формулой
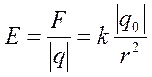 |
что и напряженность поля точечного заряда, помещенного в центре сферы:
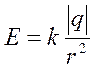 |
(1)
Внутри проводящего шара (r<R) напряженность поля равна нулю. В этом мы скоро убедимся.
Картина силовых линий наглядно показывает, как направлена напряженность электрического поля в различных точках пространства. По изменению густоты линий можно судить об изменении модуля напряженности поля при переходе от точки к точке.
 |  | ||||
 | |||||
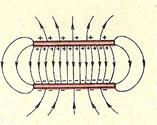
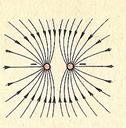
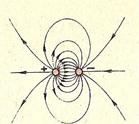 Рис.1 Рис.2 Рис.3
Рис.1 Рис.2 Рис.3
Рис.4 Рис.5 Рис.6
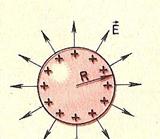 | 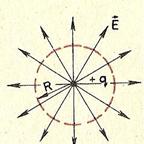 | ||
Рис.7 Рис.8
ПРОВОДНИКИ В ЭЛЕКТРОСТАТИЧЕСКОМ ПОЛЕ
Что происходит с телами, если их зарядить или поместить в электрическое поле? Проще всего ответить на этот вопрос в случае проводника. В проводниках есть свободные заряды.
Свободные заряды, В проводниках, к которым в первую очередь относятся металлы, имеются заряженные частицы, способные перемещаться внутри проводника под влиянием электрического поля. По этой причине заряды этих частиц называют свободными зарядами.
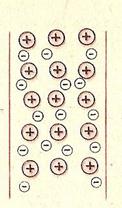
В металлах носителями свободных зарядов являются электроны. При образовании металла его нейтральные атомы начинают взаимодействовать друг с другом. Благодаря этому взаимодействию электроны внешних оболочек атомов полностью утрачивают связи со своими атомами и становятся «собственностью» всего проводника в целом. В результате образовавшиеся положительно заряженные ионы оказываются окруженными отрицательно заряженным «газом», образованным коллективизированными электронами (рис. 1). Свободные электроны участвуют в тепловом движении и могут перемещаться по куску металла в любом направлении.
Электростатическое поле внутри проводника. Наличие в проводнике свободных зарядов приводит к тому, что внутри проводника электростатического поля нет. Если бы напряженность электрического поля была отлична от нуля, то поле приводило бы свободные заряды в упорядоченное движение, т. е. в проводнике существовал бы электрический ток. Утверждение об отсутствии электростатического поля внутри проводника справедливо как для заряженного проводника, так и для незаряженного, помещенного во внешнее электростатическое поле. На примере незаряженной пластины (проводника), внесенной в однородное поле (рис. 2), выясним, в результате какого процесса напряженность электростатического поля внутри проводника оказывается равной нулю.
Под действием электрического поля электроны пластины начинают перемещаться справа налево. В первый момент (при внесении пластины в поле) возникает электрический ток. Левая часть пластины заряжается отрицательно, а правая — положительно. В этом состоит явление электростатической индукции. (Если разделить пластину пополам вдоль линии MN, то обе половины окажутся заряженными.) Появившиеся заряды - создают свое поле (линии напряженности этого поля показаны на рисунке 3 пунктирными прямыми), которое накладывается на внешнее поле и компенсирует его. За ничтожно малое время заряды перераспределяются так, что напряженность результирующего поля внутри пластины становится равной нулю и движение зарядов прекращается. Иначе в проводнике все время протекал бы ток, и выделялась теплота. Но согласно закону сохранения энергии это невозможно.
Итак, электростатического поля внутри проводника нет. На этом факте основана так называемая электростатическая защита. Чтобы защитить чувствительные к электрическому полю приборы, их заключают в металлические ящики.
Силовые линии электростатического поля вне проводника в непосредственной близости к его поверхности перпендикулярны поверхности. Если бы это было не так, то имелась бы составляющая напряженности поля вдоль поверхности проводника и по поверхности протекал бы ток.
Электрический заряд проводников. Внутри проводника при равновесии зарядов не только напряженность поля равна нулю, равен нулю и заряд. Весь статический заряд проводника сосредоточен на его поверхности. В самом деле, если бы внутри проводника имелся бы заряд, то вблизи заряда имелось бы и поле. Но электростатического поля внутри проводника нет. Следовательно, заряды в проводнике могут располагаться только на его поверхности. Этот вывод справедлив как для незаряженных проводников в электрическом поле, так и для заряженных. Отсутствие заряда внутри проводника можно обнаружить с помощью простых опытов, например опыта с цилиндром из проволочной сетки (рис. 4). На поверхности цилиндра наклеены легкие листочки станиоля. На проводящем подвижном стержне, проходящем сквозь цилиндр, укреплены еще два листочка. Если сообщить цилиндру заряд, например, от электростатической машины, листочки отклонятся на некоторый угол, так как перетекший на них заряд будет отталкиваться от одноименного заряда цилиндра или соседнего листочка. Но если листочки на стержне ввести внутрь цилиндра, то они не отклонятся, так как заряд на них равен нулю.
При равновесии зарядов электрическое поле и электрический заряд внутри проводника равны нулю. Весь заряд сосредоточен на поверхности проводника, а линии напряженности электрического поля в любой точке поверхности проводника перпендикулярны этой поверхности.
 | |||||
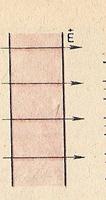 |  |
Рис.1 Рис.2 Рис.3
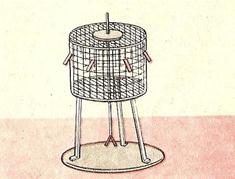 |
Рис.4
 2015-03-07
2015-03-07 5709
5709








